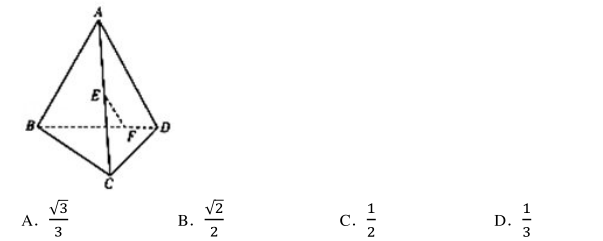





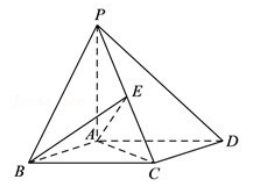
如图, 四棱锥 P﹣ ABCD 的底面 ABCD 是平行四边形, PA⊥底面 ABCD, PA=AD=4, ∠BAD=120° , 平行四边形 ABCD 的面积为4√3, 设 E 是侧棱 PC 上一动点.
(1) 求证: CD⊥AE;
(2) 当 E 是棱 PC 的中点时, 求点 C 到平面 ABE 的距离.
在锐角△ABC 中, B=60° , AB=3, AC= √7.
(1) 求△ABC 的面积;
(2) 延长边 BC 到 D, 使得 BD=4BC, 求 sin∠ADB.
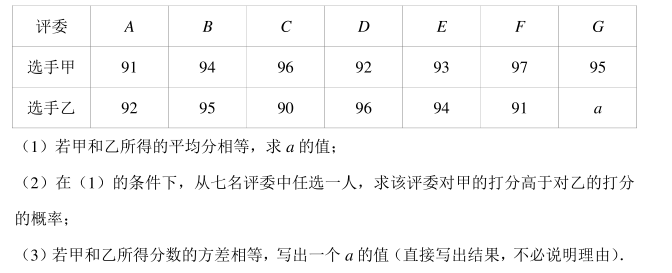
某校举办歌唱比赛, A~G 七名评委对甲、 乙两名选手打分如表所示:
已知三棱锥 P﹣ ABC 的每条侧棱与它所对的底面边长相等, 且PA= 3√2, PB=PC=5, 则该三棱锥的外接球的表面积为 .



如图, 在正四面体 ABCD 中, E 是棱 AC 的中点, F 在棱 BD 上, 且 BD=4FD,则异面直线 EF 与 AB 所成的角的余弦值为()