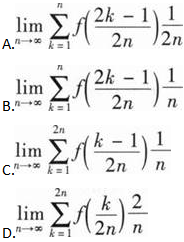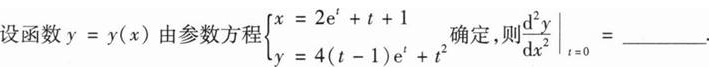
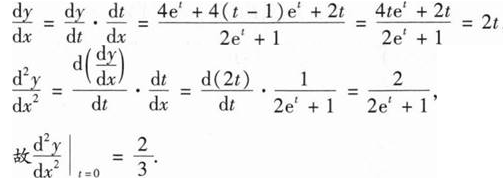
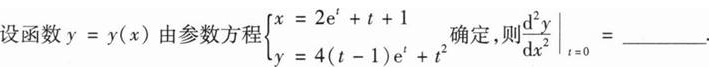
在区间(0，2)上随机取一点，将该区间分成两段，其中较短一段的长度记为X，较长一段的
长度记为Y，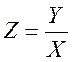
．
(Ⅰ)求X的概率密度；
(Ⅱ)求Z的概率密度；
(Ⅲ)求E(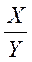
)．
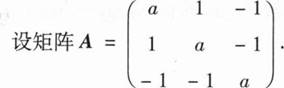
(Ⅰ)求正交矩阵P，使PTAP为对角矩阵；
(Ⅱ)求正定矩阵C，使C2=(a+3)E-A，其中E为三阶单位矩阵．
设DR2是有界单连通闭区域，
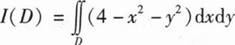
取得最大值的积分区域记为D1
(Ⅰ)求I(D1)的值；
(Ⅱ)
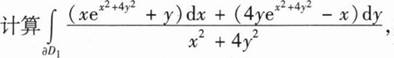
其中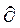
D1是D1的正向边界．
已知曲线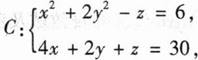
求C上的点到xOy坐标平面距离的最大值．
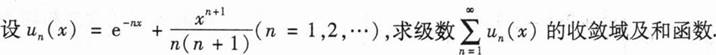
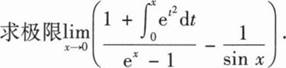
设X1，X2，…，X16是来自总体N(μ，4)的简单随机样本，考虑假设检验问题：H0：μ≤10，H1：μ>10．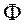
(x)表示标准正态分布函数．若该检验问题的拒绝域为
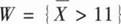，其中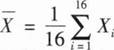
，则μ=11．5时，该检验犯第二类错误的概率为（ ）．
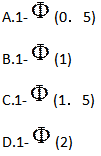
设函数f(x)在区间[0，1]上连续，则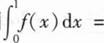
（ ）．
