设F为抛物线C:y²=4x的焦点，点A在C上，点B(3,0)，若|AF|=|BF|， 则|AB|=

• A.2
• B.2√2
• C.3
• D.3√2

答案： B

本题解析：

更新时间：2022-06-09 09:40

纠错

包含此试题的试卷

• 2022年普通高等学校招生全国统一考试理科数学乙卷

你可能感兴趣的试题

单选题

设F为抛物线C:y²=4x的焦点，点A在C上，点B(3,0)，若|AF|=|BF|， 则|AB|=

• A.2
• B.2√2
• C.3
• D.3√2

查看答案

单选题

嫦娥二号卫星在完成探月任务后，继续进行深空探测，成为我国第一颗环绕太阳飞行的人造卫星为研究嫦娥二号绕日周期与地球绕日周期的比值，用到数列{b_n}

• A.A
• B.B
• C.C
• D.D

查看答案

单选题

• A.-2
• B.-1
• C.1
• D.2

查看答案

单选题

• A.a=1,b=-2
• B.a=-1,b=2
• C.a=1,b=2
• D.a=-1,b=-2

查看答案

单选题

设全集U={1,2,3,4,5}，集合M满足C_UM={1,3}，则

• A.2∈M
• B.3∈M
• C.4∉M
• D.5∉M

查看答案

问答题

查看答案

问答题

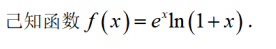
(I) 求曲线y= f(x)在点(0,f(0))处的切线方程;

(II)设g(x)= f"(x)，讨论函数g(x)在[0,+∞).上的单调性;

(II)证明:对任意的s,t∈(0,+∞)，有f(s+t)> f(s)+ f(t).

查看答案

问答题

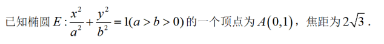
(I) 求椭圆E的方程:

(Ⅱ)过点P(-2,1)作斜率为h的直线与椭圆E交于不同的两点B,C，直线4B,.4C分别与x轴交于点M,N，当|MN|=2时，求k的值.

查看答案

问答题

在校运动会.上，只有甲、乙、丙三名同学参加铅球比赛，比赛成绩达到9.50m以上(含9.50m)的同学将获得优秀奖，为预测获得优秀奖的人数及冠军得主，收集了甲、乙、丙以往的比赛成绩，并整理得到如下数据（单位：m）：

甲: 9.80, 9.70, 9.55, 9.54, 9.48, 9.42, 9.40, 9.35, 9.30, 9.25;

乙: 9.78, 9.56, 9.51, 9.36, 9.32, 9.23;

丙: 9.85, 9.65, 9.20, 9.16.

假设用频率估计概率，且甲、乙、丙的比赛成绩相互独立

(I)估计甲在校运动会铅球比赛中获得优秀奖的概率;

(II) 设X是甲、乙、丙在校运动会铅球比赛中获得优秀奖的总人数，估计X的数学期望EX ;

(II)在校运动会铅球比赛中，甲、乙、丙谁获得冠军的概率估计值最大? (结论不要求证明)

查看答案

问答题

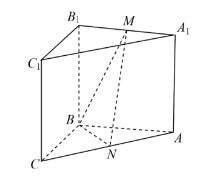
如图，在三棱柱ABC-A1B1C1中，侧面BCC1B1为正方形，平面BCC1B1⊥平面ABB1A1，AB=BC=2，M，N分别为A1B1，AC的中点

（1）求证：MN∥BCC1B1

（2）(I)再从条件①、条件②这两个条件中选择-一个作为已知，求直线AB与平面BMN所成角的正弦值。

条件①:AB⊥MN;

条件②: BM = MN.

注:如果选择条件①和条件②分别解答，按第一个解答计分。

查看答案