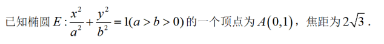
(I) 求椭圆E的方程:
(Ⅱ)过点P(-2,1)作斜率为h的直线与椭圆E交于不同的两点B,C，直线4B,.4C分别与x轴交于点M,N，当|MN|=2时，求k的值.
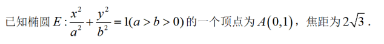
(I) 求椭圆E的方程:
(Ⅱ)过点P(-2,1)作斜率为h的直线与椭圆E交于不同的两点B,C，直线4B,.4C分别与x轴交于点M,N，当|MN|=2时，求k的值.
在校运动会.上，只有甲、乙、丙三名同学参加铅球比赛，比赛成绩达到9.50m以上(含9.50m)的同学将获得优秀奖，为预测获得优秀奖的人数及冠军得主，收集了甲、乙、丙以往的比赛成绩，并整理得到如下数据（单位：m）：
甲: 9.80, 9.70, 9.55, 9.54, 9.48, 9.42, 9.40, 9.35, 9.30, 9.25;
乙: 9.78, 9.56, 9.51, 9.36, 9.32, 9.23;
丙: 9.85, 9.65, 9.20, 9.16.
假设用频率估计概率，且甲、乙、丙的比赛成绩相互独立
(I)估计甲在校运动会铅球比赛中获得优秀奖的概率;
(II) 设X是甲、乙、丙在校运动会铅球比赛中获得优秀奖的总人数，估计X的数学期望EX ;
(II)在校运动会铅球比赛中，甲、乙、丙谁获得冠军的概率估计值最大? (结论不要求证明)
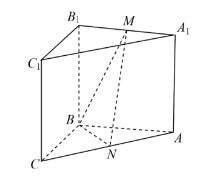
如图，在三棱柱ABC-A1B1C1中，侧面BCC1B1为正方形，平面BCC1B1⊥平面ABB1A1，AB=BC=2，M，N分别为A1B1，AC的中点
（1）求证：MN∥BCC1B1
（2）(I)再从条件①、条件②这两个条件中选择-一个作为已知，求直线AB与平面BMN所成角的正弦值。
条件①:AB⊥MN;
条件②: BM = MN.
注:如果选择条件①和条件②分别解答，按第一个解答计分。
在△ABC中，sin2C= √3 sinC.
(I)求∠C:
(II)若b=6，且△ABC的面积为6√3，求△ABC的周长.
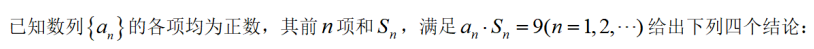
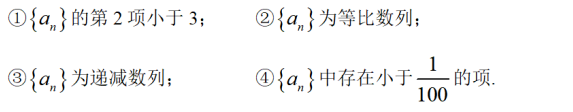
其中所有正确结论的序号是
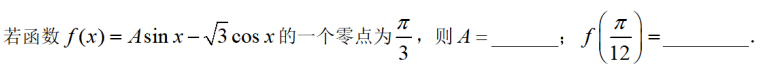
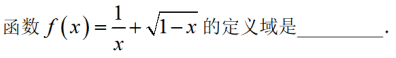
在△ABC中，AC=3，BC=4，∠C=90°，P为△ABC所在平面内的动点，且PC=1，则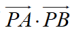
的取值范围是
