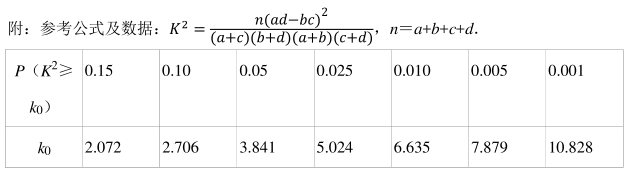
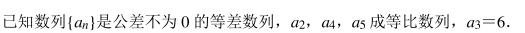霍兰德职业能力测试问卷可以为大学生在择业方面提供参考, 对人的能力兴趣等方面进行评估. 某大学随机抽取 100 名学生进行霍兰德职业能力测试问卷测试, 测试结果发现这 100 名学生的得分都在[50, 100]内, 按得分分成 5 组: [50, 60), [60, 70), [70, 80),[80, 90), [90, 100], 得到如图所示的频率分布直方图, 则这 100 名同学得分的中位数为()
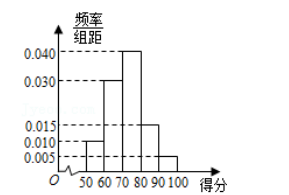


霍兰德职业能力测试问卷可以为大学生在择业方面提供参考, 对人的能力兴趣等方面进行评估. 某大学随机抽取 100 名学生进行霍兰德职业能力测试问卷测试, 测试结果发现这 100 名学生的得分都在[50, 100]内, 按得分分成 5 组: [50, 60), [60, 70), [70, 80),[80, 90), [90, 100], 得到如图所示的频率分布直方图, 则这 100 名同学得分的中位数为()

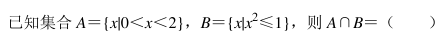
若 z(1﹣ i) =4i, 则|z|=()
已知函数 f(x) =2|x﹣ 1|﹣ |x+1|.
(1) 在答题卡所给出的网格坐标系中作出函数 f(x) 的图象(不要求写作法), 并直接写出函数 f(x) 的最小值;
(2) 已知函数 g(x) =|x+a|﹣ 2|x﹣ a|, 若存在 x 1 , x 2 ∈R 使 f(x 1 ) +5=g(x 2 ), 求实数a 的取值范围.


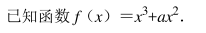


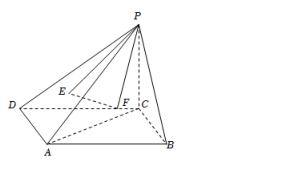
如图, 在四棱锥 P﹣ ABCD 中, ABCD 是菱形, E, F分别是△PAD, △PAB 的重心, 平面 PCD⊥平面 ABCD, 平面 PBC⊥平面 ABCD.
(1) 求证: EF∥平面 ABCD;
(2) 求证; 平面 PEF⊥平面 PAC.
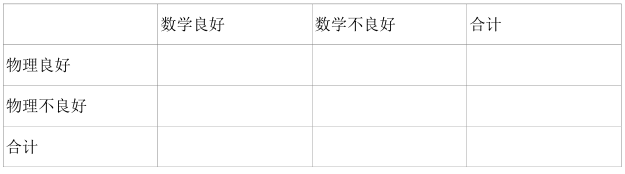
某学校高三理科实验班共计 40 名学生, 在备考复习教学中进行了 8 次规范性的考试, 将每个学生 8 次考试的数学平均分、 物理平均分制成茎叶图如下. 数学满分 150分, 达到或超过 120 分认为是良好的; 物理满分 120 分, 成绩达到或超过 96 分认为是良好的. 已知数学良好的学生中, 恰好有 4 人物理不良好
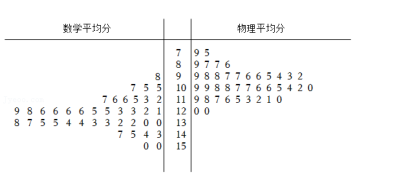
(1) 求数学成绩的众数、 中位数;
(2) 请填写下面列联表, 并根据列联表判断是否有 99.5%的把握认为学生物理良好与数学良好有关?
(3) 在物理不良好的学生中按照数学是否良好分层抽取 5 位同学, 再从这 5 位同学中抽取两位进行数学基础是否对物理学习有影响的深度访谈, 求被抽到的两位同学恰好有一位数学良好的概率.