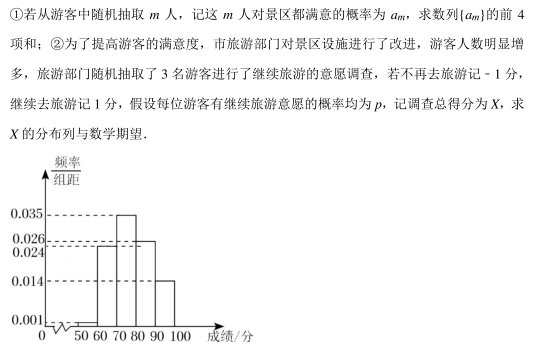
设函数 f（x） 在 R 上存在导函数 f'（x）， f（x） 的图象在点 M（1， f（1）） 处的切线方程为y=1/2x+ 2， 那么 f（1） +f'（1） ＝（）
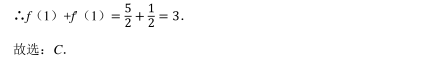
设函数 f（x） 在 R 上存在导函数 f'（x）， f（x） 的图象在点 M（1， f（1）） 处的切线方程为y=1/2x+ 2， 那么 f（1） +f'（1） ＝（）
已知等差数列{a n }的公差为 1， S n 为其前 n 项和， 若 S 3 ＝a 6 ， 则 a 2 ＝（）
在复平面内， 复数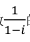
的共轭复数对应的点位于（）
已知集合 A＝{﹣ 1， 0， 1， 2}， B＝{x|x 2 ＜4}， 则 A∩ B＝（）
已知函数 f（x） ＝|x﹣ 4|+|x+3|．
（1） 求不等式 f（x） ≥12 的解集；
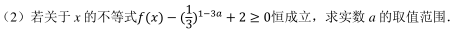
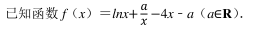
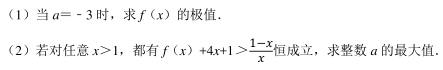
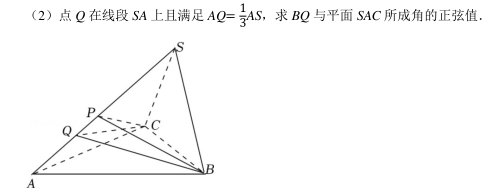
如图， 三棱锥 S﹣ ABC 中， 底面 ABC 和侧面 SBC 都是等边三角形， BC＝2，SA= √6．
（1） 若 P 点是线段 SA 的中点， 求证： SA⊥平面 PBC；
为了了解游客对景区的满意度， 市旅游部门随机对景区的 100 名游客进行问卷调查（满分 100 分）， 这 100 名游客的评分分别落在区间[50， 60）， [60， 70）， [70， 80），[80， 90）， [90， 100]内， 且游客之间的评分情况相互独立， 得到统计结果如频率分布直方图所示．
（1） 求这 100 名游客评分的平均值（同一区间的数据用该区间数据的中点值为代表）；
（2） 视频率为概率， 规定评分不低于 80 分为满意， 低于 80 分为不满意， 记游客不满意的概率为 p．
