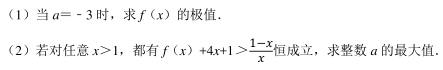
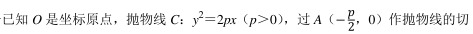
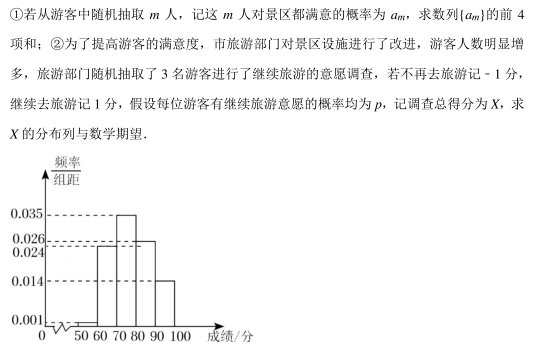
如图， 三棱锥 S﹣ ABC 中， 底面 ABC 和侧面 SBC 都是等边三角形， BC＝2，SA= √6．
（1） 若 P 点是线段 SA 的中点， 求证： SA⊥平面 PBC；
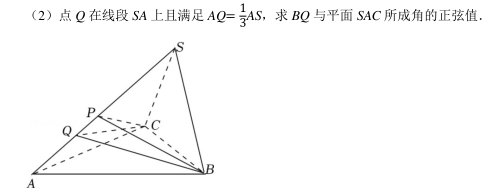
为了了解游客对景区的满意度， 市旅游部门随机对景区的 100 名游客进行问卷调查（满分 100 分）， 这 100 名游客的评分分别落在区间[50， 60）， [60， 70）， [70， 80），[80， 90）， [90， 100]内， 且游客之间的评分情况相互独立， 得到统计结果如频率分布直方图所示．
（1） 求这 100 名游客评分的平均值（同一区间的数据用该区间数据的中点值为代表）；
（2） 视频率为概率， 规定评分不低于 80 分为满意， 低于 80 分为不满意， 记游客不满意的概率为 p．
在平面直角坐标系 xOy 中， 已知直线 l： y＝kx+8 上存在点 P， 过点 P 作圆 O： x 2 +y 2 ＝4的切线， 切点分别为 A（x 1 ， y 1 ）， B（x 2 ， y 2 ）， 且 x 1 x 2 +y 1 y 2 ＝﹣ 2， 则实数 k 的取值范围为
已知 P 为球 O 球面上一点， 点 M满足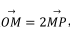
过点 M与 OP 成 30° 的平面截球 O，截面的面积为 16π， 则球 O 的表面积为
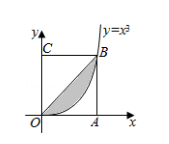
如图所示， 在边长为 1 的正方形 OABC 中任取一点 P， 则点 P 恰好取自阴影部分（由对角线 OB 及函数 y＝x3 围成） 的概率为
