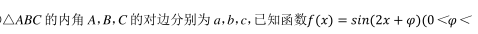
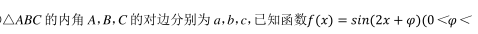
在平面直角坐标系 xOy 中， 已知直线 l： y＝kx+8 上存在点 P， 过点 P 作圆 O： x 2 +y 2 ＝4的切线， 切点分别为 A（x 1 ， y 1 ）， B（x 2 ， y 2 ）， 且 x 1 x 2 +y 1 y 2 ＝﹣ 2， 则实数 k 的取值范围为
已知 P 为球 O 球面上一点， 点 M满足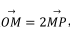
过点 M与 OP 成 30° 的平面截球 O，截面的面积为 16π， 则球 O 的表面积为
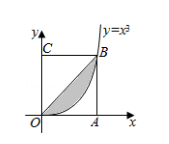
如图所示， 在边长为 1 的正方形 OABC 中任取一点 P， 则点 P 恰好取自阴影部分（由对角线 OB 及函数 y＝x3 围成） 的概率为
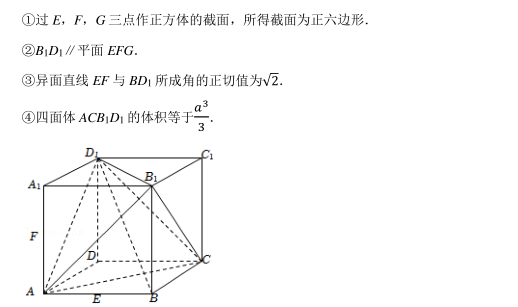
已知正方体 ABCD﹣ A 1 B 1 C 1 D 1 的棱长为 a， 点 E， F， G 分别为棱 AB， AA 1 ， C 1 D 1 的中点， 下列结论中正确的个数是（）
已知关于 x 的方程 x﹣ lna＝2ln|x|有三个不等的实数根， 则实数 a 的取值范围是（）
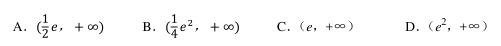
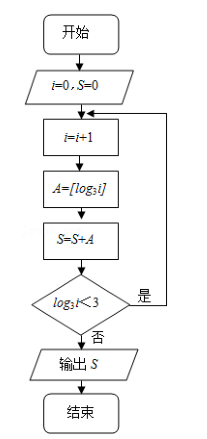
已知函数 y＝[x]称为高斯函数， 其中[x]表示不超过实数 x 的最大整数， 执行如图程序框图， 则输出的 S 值为（）
