设n元线性方程组Ax=b，其中
.
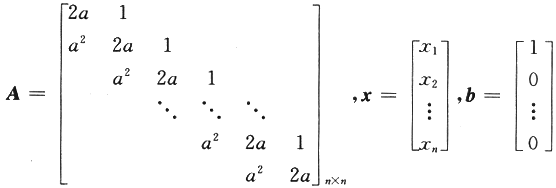
(Ⅰ)证明行列式｜A｜=(n+1)a^n；
(Ⅱ)当a为何值时，该方程组有唯一解，并求x1；
(Ⅲ)当a为何值时，该方程组有无穷多解，并求通解.
设α，β为三维列向量，矩阵A=αα^T+ββ^T，其中α^T，β^T分别是α，β的转置.证明：
(Ⅰ)秩r(A)≤2；
(Ⅱ)若α，β线性相关，则秩r(A)<2.
将函数f(x)=1-x(0≤x≤π)展开成余弦级数，并求级数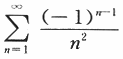
的和.
设f(x)是连续函数，
(Ⅰ)利用定义证明函数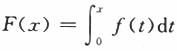
可导，且F’(x)=f(x)；
(Ⅱ)当f(x)是以2为周期的周期函数时，证明函数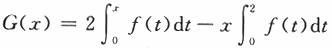
也是以2为周期的周期函数.
已知曲线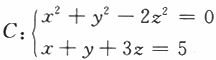
，求C上距离xOy面最远的点和最近的点.
计算曲线积分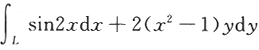
，其中L是曲线y=sinx上从点(0，0)到点(π，0)的一段.
