设α,β为三维列向量,矩阵A=αα^T+ββ^T,其中α^T,β^T分别是α,β的转置.证明:
(Ⅰ)秩r(A)≤2;
(Ⅱ)若α,β线性相关,则秩r(A)<2.
【证明】(Ⅰ)因为α,β为三维列向量,那么αα^T和ββ^T都是三阶矩阵,
且秩r(αα^T)≤1,r(ββ^T)≤1.
那么,r(A)=r(αα^T+ββ^T)≤r(αα^T)+r(ββ^T)≤2.
(Ⅱ)由于α,β线性相关,不妨设α=kβ,于是
r(A)=r(αα^T+ββ^T)=r((1+k^2)ββ^T)≤r(β)≤1<2.
【评注】本题考查矩阵秩的性质公式.
(Ⅰ)中有两个基本知识点:①r(αα^T)≤1和②r(A+B)≤r(A)+r(B).
(Ⅱ)中有两个基本知识点:①α,β线性相关的几何意义和②r(kA)=r(A),k≠0.
注意,如果分块矩阵比较熟悉,本题的(Ⅰ)也可如下处理:
因为
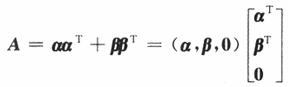
那么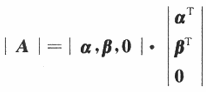
从而r(A)≤2.