2010全国硕士研究生入学考试《数学2》真题

试卷预览

1 单选题 1分

设A为4阶实对称矩阵，且A2＋A＝O。若A的秩为3，则A相似于（　　）。

查看答案 开始考试

正确答案：D

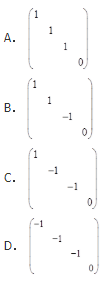
本题解析：

设λ为A的特征值，由于A2＋A＝O，所以λ2＋λ＝0，即（λ＋1）λ＝0。这样A的特征值为－1或0。由于A为实对称矩阵，故A可相似对角化，即A～Λ，r（A）＝r（Λ）＝3。

因此

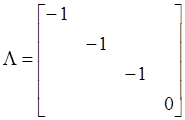
即

2 单选题 1分

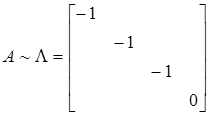
设向量组Ⅰ：α1，α2，…，αr可由向量组Ⅱ：β1，β2，…，βs线性表示，下列命题正确的是（　　）。

查看答案 开始考试

正确答案：A

本题解析：

由于向量组Ⅰ能由向量组Ⅱ线性表示，所以r（Ⅰ）≤r（Ⅱ），即r（α1，α2，…，αr）≤r（β1，β2，…，βs）≤s。若向量组Ⅰ线性无关，则r（α1，α2，…，αr）＝r，所以r（α1，α2，…，αr）≤r（β1，β2，…，βs）≤s。即r≤s，选A项。

3 单选题 1分

查看答案 开始考试

正确答案：D

本题解析：

4 单选题 1分

设m，n为正整数，则反常积分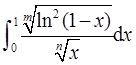的收敛性（　　）。

查看答案 开始考试

正确答案：D

本题解析：

分析过程如下。根据题目有

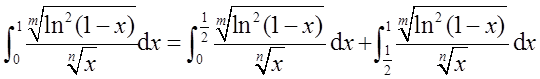
①对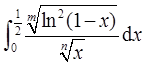进行讨论：被积函数只在x→0＋时无界。因为

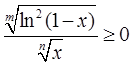
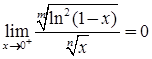
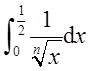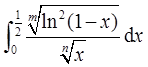又反常积分收敛，所以收敛。

②对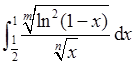进行讨论：被积函数只在x→1－时无界。因为

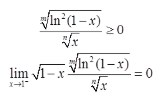
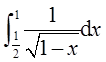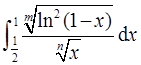且反常积分收敛，所以收敛。

综上，无论正整数m和n取何值，反常积分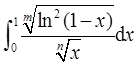都收敛，故选D。

5 单选题 1分

设y1，y2是一阶线性非齐次微分方程y′＋p（x）y＝q（x）的两个特解，若常数λ，μ使λy1＋μy2是该方程的解，λy1－μy2是该方程对应的齐次方程的解，则（　　）。

查看答案 开始考试

正确答案：A

本题解析：

因λy1－μy2是y′＋p（x）y＝0的解，故（λy1－μy2）′＋p（x）（λy1－μy2）＝0。所以λ（y1′＋p（x）y1）′－μ（y2′＋p（x）y2）＝0。而由y1′＋p（x）y1＝q（x），y2′＋p（x）y2＝q（x），所以有（λ－μ）q（x）＝0。

又因λy1＋μy2是非齐次y′＋p（x）y＝q（x）的解，故（λy1＋μy2）′＋p（x）（λy1＋μy2）＝q（x）。所以（λ＋μ）q（x）＝q（x）。故λ＝μ＝1/2。

6 单选题 1分

设函数z＝z（x，y）由方程F（y/x，z/x）＝0确定，其中F为可微函数，且F2′≠0，则x·（?z/?x）＋y·（?z/?y）＝（　　）。

查看答案 开始考试

正确答案：B

本题解析：

由F（y/x，z/x）＝0得

7 单选题 1分

曲线y＝x2与曲线y＝alnx（a≠0）相切，则a＝（　　）。

查看答案 开始考试

正确答案：C

本题解析：