推荐等级:
发布时间: 2021-12-30 16:26
扫码用手机做题
设函数f(x),g(x)的2阶导函数在x=a处连续,则
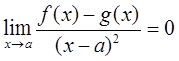
是两条曲线y=f(x),y=g(x)在x=a对应的点处相切及曲率相等的( )。
本题解析:
①充分性
在x=a处,由泰勒公式得
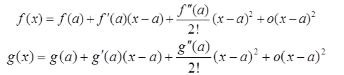
代入
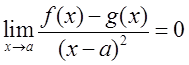
可得f(a)=g(a),f′(a)=g′(a),f″(a)=g″(a),因此两条曲线在x=a处相切且斜率相等。
②必要性
必要性不成立。例如f(x)=(x-a)2,g(x)=-(x-a)2,它们在点a相切且具有相同的曲率,但
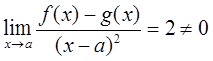
故选A。
试卷分类:学硕教育学
练习次数:0次
试卷分类:学硕心理学
练习次数:0次
试卷分类:管理类联考综合
练习次数:0次
试卷分类:法硕非法学
练习次数:0次
试卷分类:法硕法学
练习次数:0次
试卷分类:西医综合
练习次数:0次
试卷分类:政治
练习次数:0次
试卷分类:中医综合
练习次数:0次
试卷分类:431金融学综合
练习次数:4次
试卷分类:431金融学综合
练习次数:7次