人格的核心是( )。
人格的核心是性格。
义务教育教科书《数学》四年级上册(人教版)关于平行的教学内容阅览并回答问题。
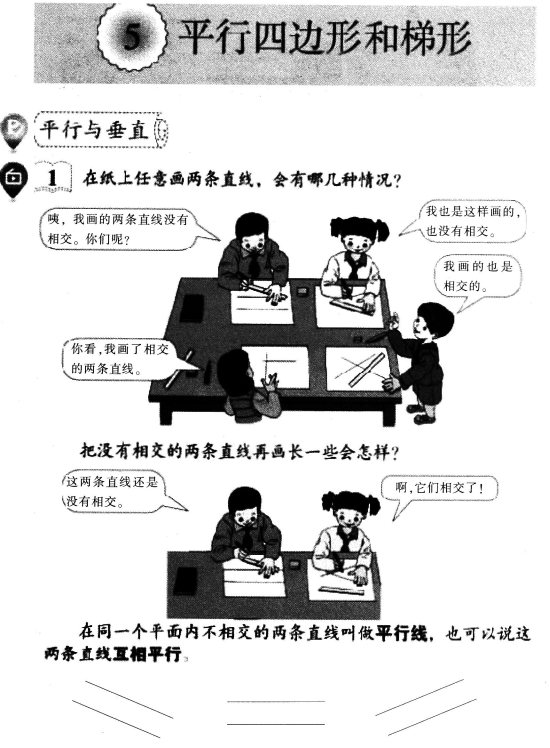
上图中a和b互相平行,记做a∥b,读作a平行于b。

(1)在学习本内容前,学生已具备了哪些相关知识和数学活动经验。(3分)
(2)分析“你能举出生活中一些有关平行的例子吗”这句话的编写意图。(3分)
(3)写出本内容的教学重点和教学难点。(4分)
(4)设计本内容的教学过程。(10分)
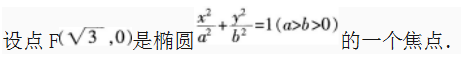
且与椭圆短轴的两个端点组成等边三角形。
(1)求椭圆的方程;
(2)过点F作一直线l交椭圆于A,B两点,设F1为椭圆的另一个焦点,当 △F1AB的面积最大时,求l的方程。
已知函数f(x)=㏑(x+2)-x2+bx+c,
(1)若点P(-1,0)在f(x)的图象上,过点P的切线与直线y=-x+2平行,求f(x)的解析式;
(2)若f(x)在区间[0,2]上单调递增,求b的取值范围。
如图,在△ABC中,AC=8,BC=6,∠ACB=90°,动点P以每秒一个单位的速度从点A出发,沿着边AC向点C移动,同时,动点Q以相同的速度从点B出发,沿着边BA向点A移动,设P,Q两点移动时间为t秒(0≤t≤8)。
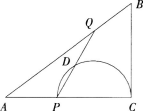
(1)当t为何值时,△APQ的面积最大 最大值是多少
(2)以PC为直径的半圆交PQ于点D,是否存在t,使得PD=DQ 若存在,求出t的值,若不存在说明理由。
有一群鸽子和一些鸽笼,如果每个鸽笼可住6只鸽子,则剩下3只鸽子无鸽笼;如果再飞来5只鸽子,连同原来的鸽子,每个鸽笼刚好住8只,问原来多少鸽子和鸽笼
在“异分母分数加减法”的课后作业中,有的学生出现这样的错误:
(1)分析导致错误的原因;
(2)针对错误原因,给出教学建议。
在“3的倍数的特征”一课中,教师通常让学生在百数表中圈出所有3的倍数,再引导学生从不同角度观察所圈数的特征,最后得出3的倍数的特征,这样的推理是________。
若(2x+1)n=a0+a1x+a2x2+a3x3+…+anxn,且a0+a1+a2+a3+…+an=81,则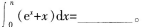
若乙数是甲数的3/4.丙数是乙数的4/5,则甲:乙:丙=________
杨老师在教学《平行四边形的面积》一课的最后环节,不仅让学生强化记忆了平行四边形的面积公式,还结合板书引导学生对公式的推导过程进行回顾反思。对其评价不恰当的是( )。