当前位置:首页 → 职业资格 → 教师资格 → 中学数学学科知识与教学能力->案例:“三角形中位线定理”是八年级学生的学习内容,下面是两位
案例:“三角形中位线定理”是八年级学生的学习内容, 下面是两位教师的教学片段:
(一)教师甲
在讲授中位线定理这一内容时,利用“数学软件A ”作了两次测量,一次是验证三角形中位线定理,另一次是验证顺次连接四边形的中点所围成的图形为平行四边形。教师甲发现,当他让学生动手测量的时候,有一部分学生懒散地坐着,没有刚开始接触该软件时那样积极,课后教师向几位同学询问情况,有学生说这两道题书上都有结论,早就看过了,再去测量是不是有点儿傻?
(2)教师乙
教师首先让学生探究问题,如图 2,五边形 ABCDE 中,点F、G、H、I分别是 AB、BC、CD、DE的中点, J、K分别是FH、JI的中点, AE 与 JK 有什么关系?
学生们马上打开“数学软件 A ”进行测量,很快发现 AE=4JK能不能证明发现的结论呢?学生们没有一点头绪。
教师提示说当遇到问题解决不了的时候,我们是不是进一步先解决容易的问题?教师引导学生去研究三角形中位线定理和顺次连接四边形中点所围成的图形是平行四边形两个问题,经过师生的共同研究,取 AD 的中点C 后,学生不仅验证了 AE
而且高兴地发现 AE 和JK 还存在平行关系,如图 3。
问题:(1)请分别对教师甲和乙的教学进行评价;(10 分)
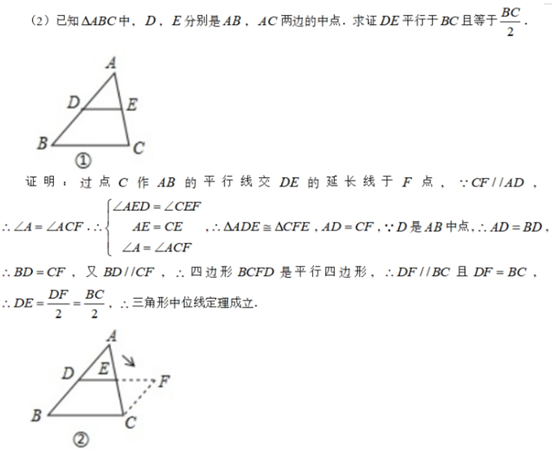
(2)请画出适用于本节课教学的“三角形中位线定理”证明的示意图(图中辅助线用虚线表示);(5 分)
(3)结合本案例,请谈谈信息技术在数学中的作用。(5 分)
(1)教师甲没有遵循学生由易到难的认知顺序,不利于学生的学习.这位教师在教学过程中先借助信息技术,学生直观观察,可以获得一定的结论,之后再让学生自行测量就会给学生一种先难后易的感觉,学生很难进入学习的状态,也很难继续对知识产生兴趣.
教师乙先是借助一个比较困难的问题,学生通过思考,发现不能用已有知识解决这样的问题,此时教师提出,可以从简单的问题入手,从三角形中位线定理和四边形中点构成平行四边形入手,结合信息技术帮助学生直观观察,更好的理解.这位老师的借助困难的问题引出学生想要学习的欲望,再用简单的问题给学生信心,最后借助信息技术,呈现与五边形有关的问题,水到渠成,实现了本节课的教学目标.
(3)信息技术的发展对数学教育的价值、目标、内容以及教学方式产生了很大的影响.数学课程的设计与实施应根据实际情况合理地运用现代信息技术.它可以更好、更便捷展示绘制图象,图形的运动过程,数据的呈现与随机模拟结果等教学环节.
在三角形中位线定理证明的过程中,教师可以利用几何画板画出更加的准确的图形.同时本节课定理的证明主要需要的就是三角形底边与中位线之间的数量关系与平行关系.首先,利用几何画板可以轻松地测量出线段的长短,这要比手动画图更加准确;而平行关系的证明,则可以通过对应角之间的关系进一步推证,几何画板可以直接标注出角的大小,方便学生观察直接得出结论.同时,定理的证明并不依赖于一个图形得出,使用几何画板可以改变三角形的形状,方便学生得出一般结论.
但是教师在使用信息技术的时候应该注意使用的时机和程度,信息技术的应用应该是对数学教学的一种辅助,是为了更好地帮助学生理解在实际操作中不好实现的作图问题或者是较多数据的呈现,注意不要太过于依赖信息技术而忽略的自身的讲解,避免分散学生太多的注意力,要注意信息技术与传统教学相结合,为学生提供更好地教学环境.
教师职业道德区别于其他职业道德的显著标志就是( )。
教师在直观教学时,应用“变式”方法的目的在于( )。
《普通高中数学课程标准(实验)》提出五种基本能力,没有包含在其中的是
在教学过程中,教师指导学生体验客观事物的真善美的方法是( )。
在学校教育依照特定教学目标组织教学的过程中,起关键作用的是( )。
被毛泽东主席誉为“一代天骄”的成吉思汗( )
"三五步行遍天下,六七人百万雄兵”描写的是( )。
简述学习动机的分类。
简述学生心理发展的基本特征。
在教育史上主张“不愤不启,不悱不发”的教育家是()。