当前位置:首页 → 职业资格 → 教师资格 → 中学数学学科知识与教学能力->为例,说明在教学中如何体现该教学原则。
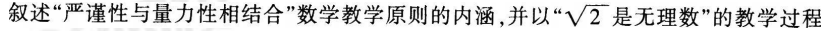
为例,说明在教学中如何体现该教学原则。
(1)数学的严谨性,是指数学具有很强的逻辑性和较高的精确性,即逻辑的严格性和结论的确定性。量力性是指学 生的可接受性。 这一原则,说明教学中的数学知识的逻辑严谨性与学生的可接受性之间相适应的关系。理论知识的严谨程度要适合 学生的一般知识结构与智力发展水平,随着学生知识结构的不断完善,心理发展水平的提高,逐渐增强理论的严谨 程度;反过来,又要通过恰当的理论严谨性逐渐促进学生的接受能力。 显然,这一原则是根据数学本身的特点及学生心理发展的特点提出的。但是,在学习过程中,学生的心理发展是逐 步形成的,不同的年龄阶段,其感知、记忆、想象、思维、能力等心理因素都有不同的发展水平。这种心理发展的 渐变性决定了在教学中不可能对数学理论的研究达到完全严密的程度,而应该在不同的教学阶段,依据不同的教学 目的和内容而提出不同的严谨性要求,即数学教学的严谨性是相对的。

高其严谨程度,要求做到推理有据,证明要步步有根据、处处有逻辑。在推理有据的同时并不排斥直观和猜想,强 调思维的严谨性,允许猜想,辩证地处理好推理的依据和猜想的关系。 由于学生对无理数不熟悉,在实际教学过程中我们采用反证法,先假设是有理数。教学中可以由教师给出证明步 骤.让学生只填每一步的理由,鼓励学生发扬“跳一跳够得到”的精神,逐步过渡到学生自己给出严格证

在教学过程中,不能消极适应学生,降低理论要求,必须在符合内容科学性的前提下,结合学生实际组织教学。
《义务教育数学课程标准(2011年版)》强调,课程内容要反映社会的需要、数学的特点,要符合学生的认知规律。课程内容的组织要重视过程,处理好()的关系。
设α是某一方程组的解向量,k为某一常数,则kα也为该方程组的解向量。( )

案例:
在有理数运算的课堂教学片段中,某学生的板演如下:

针对该学生的解答,教师进行了如下教学:
师:请仔细检查你的演算过程,看是否正确无误?
生:好像正确吧。

请分析例题1、例题2中每一步运算的依据。(10分)
初中数学课程是一门国家课程,其主要内容包括课程目标、教学内容、教学过程和( )等
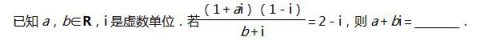
教师职业道德区别于其他职业道德的显著标志就是( )。
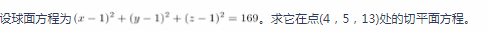
对高中数学的评价,下列说法错误的是( )。
