设 m、 n 是两条不同的直线, α、β 是两个不同的平面, 给出下列四个命题:
①若 m⊥α, n∥α, 则 m⊥n;
②若 m∥n, n∥α, 则 m∥α;
③若 m∥n, n⊥β, m∥α, 则 α⊥β;
④若 m∩ n=A, m∥α, m∥β, n∥α, n∥β, 则 α∥β.
其中真命题的个数是()

设 m、 n 是两条不同的直线, α、β 是两个不同的平面, 给出下列四个命题:
①若 m⊥α, n∥α, 则 m⊥n;
②若 m∥n, n∥α, 则 m∥α;
③若 m∥n, n⊥β, m∥α, 则 α⊥β;
④若 m∩ n=A, m∥α, m∥β, n∥α, n∥β, 则 α∥β.
其中真命题的个数是()

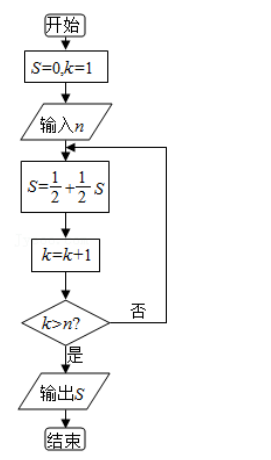
庄子说: 一尺之锤, 日取其半, 万世不竭. 这句话描述的是一个数列问题. 现用程序框图描述, 如图所示, 若输入某个正数 n后, 输出的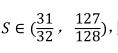 则输入的 n的值为()
则输入的 n的值为()

已知全集为 U, 集合 A, B 为 U的子集, 若(∁ U A) ∩ B=∅, 则 A∩ B=()
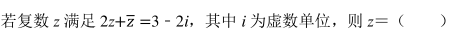
已知函数 f(x) =|x﹣ 2|+|x+1|.
(1) 解关于 x 的不等式 f(x) ≤5;



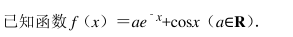

阿基米德(公元前 287 年﹣ 公元前 212 年, 古希腊) 不仅是著名的哲学家、 物理学家, 也是著名的数学家, 他利用“逼近法” 得到椭圆的面积除以圆周率 π 等于椭圆的长半轴长与短半轴长的乘积. 在平面直角坐标系 Oxy 中, 椭圆 C: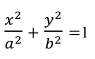 (a>b>0) 的面积为 2√3π, 两焦点与短轴的一个顶点构成等边三角形. 过点(1, 0) 的直线l 与椭圆 C 交于不同的两点 A, B.
(a>b>0) 的面积为 2√3π, 两焦点与短轴的一个顶点构成等边三角形. 过点(1, 0) 的直线l 与椭圆 C 交于不同的两点 A, B.
(1) 求椭圆 C 的标准方程;
(2) 设椭圆 C 的左、 右顶点分别为 P, Q, 直线 PA 与直线 x=4 交于点 F, 试证明 B, Q,F 三点共线;
(3) 求△AOB 面积的最大值.