我们非常熟悉: “直角三角形的两直角边的平方和等于斜边的平方”, 这个规律在中国被称为勾股定理, 勾股定理是几何学中一颗璀璨夺目的明珠, 被称为“几何学的基石”, 而且在高等数学和其他学科中也有着极为广泛的应用. 世界上的几个文明古国都发现过此定理并且进行了广泛深入的研究, 因此有许多名称, 譬如古希腊毕达哥拉斯发现研究过此定理, 又称为毕达哥拉斯定理. 中国是发现和研究勾股定理最古老的国家之一, 中国古代数学家称直角三角形为勾股形, 较短的直角边称为勾, 另一直角边称为股, 斜边称为弦, 所以勾股定理也称为勾股弦定理. 如果一个勾股形的“勾”“股”“弦” 都是整数,其中“勾” 等于 11, 那么这个勾股形的周长等于()

我们非常熟悉: “直角三角形的两直角边的平方和等于斜边的平方”, 这个规律在中国被称为勾股定理, 勾股定理是几何学中一颗璀璨夺目的明珠, 被称为“几何学的基石”, 而且在高等数学和其他学科中也有着极为广泛的应用. 世界上的几个文明古国都发现过此定理并且进行了广泛深入的研究, 因此有许多名称, 譬如古希腊毕达哥拉斯发现研究过此定理, 又称为毕达哥拉斯定理. 中国是发现和研究勾股定理最古老的国家之一, 中国古代数学家称直角三角形为勾股形, 较短的直角边称为勾, 另一直角边称为股, 斜边称为弦, 所以勾股定理也称为勾股弦定理. 如果一个勾股形的“勾”“股”“弦” 都是整数,其中“勾” 等于 11, 那么这个勾股形的周长等于()
已知直线 l 1 , l 2 , l 1 ⊥l 2 于点 H, A∈l 1 且|AH|=36, B∈l 2 , 点 M 在线段 AB 的垂直平分线上且 MB⊥l 2 , 则|MA|的最小值为()
在△ABC 中, AB= √2, BC= √3, CA=2, 则△ABC 外接圆的面积为()


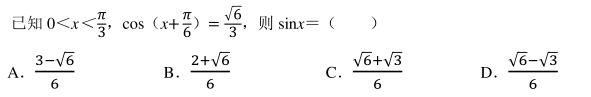
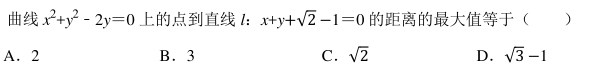
设样本数据 1, 2, x, 4, 5 的均值等于 4, 则数据 5, 11, 7, x, 10, 6, 9 的标准差等于()
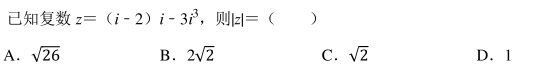
集合 M={x∈R|0<x≤2022}, N={x|x=2k, k∈Z}, 则 M∩ N 所含元素个数为()
已知函数 f(x) =|2x﹣ 1|+|2x+1|, 记不等式 f(x) <4 的解集为 M.
(1) 求 M;
(2) 设 a, b∈M, 证明: |ab|﹣ |a|﹣ |b|+1>0.