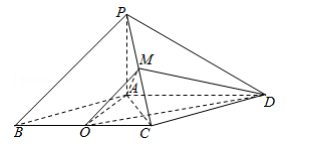
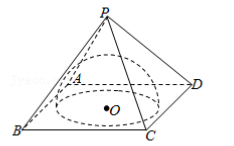
如图, 在四棱锥 P﹣ ABCD 中, 四边形 ABCD 为平行四边形, 以 BC 为直径的圆 O(O 为圆心) 过点 A, 且 AO=AC=AP=2, PA⊥底面 ABCD, M为 PC 的中点.
(1) 证明: 平面 OAM⊥平面 PCD;
(2) 求二面角 O﹣ MD﹣ C 的余弦值.

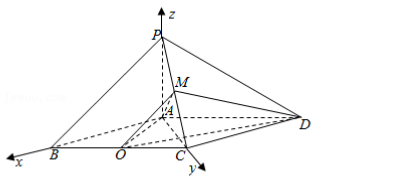
如图, 在四棱锥 P﹣ ABCD 中, 四边形 ABCD 为平行四边形, 以 BC 为直径的圆 O(O 为圆心) 过点 A, 且 AO=AC=AP=2, PA⊥底面 ABCD, M为 PC 的中点.
(1) 证明: 平面 OAM⊥平面 PCD;
(2) 求二面角 O﹣ MD﹣ C 的余弦值.

某社区为丰富居民的业余文化生活, 打算在周一到周五连续为该社区居民举行“社区音乐会”, 每晚举行一场, 但若遇到风雨天气, 则暂停举行. 根据气象部门的天气预报得知, 在周一到周五这五天的晚上, 前三天每天出现风雨天气的概率均为 p 1 , 后两天每天出现风雨天气的概率均为 p 2 , 每天晚上是否出现风雨天气相互独立已知前两天的晚上均出现风雨天气的概率为1/4,且这五天至少有一天晚上出现风雨天气的概率为199/200

△ABC 的内角 A, B, C 所对的边分别为 a, b, c, 已知 a= √3, b=2.

如图, 正四棱锥 P﹣ ABCD 的每个顶点都在球 M的球面上, 侧面 PAB 是等边三角形. 若半球 O 的球心为四棱锥的底面中心, 且半球与四个侧面均相切, 则半球 O 的体积与球 M的体积的比值为
复数 z=(1﹣ 2i)(1﹣ 5i) 的实部为 .



在三棱柱 ABC﹣ A 1 B 1 C 1 中, D 为侧棱 CC 1 的中点, 从该三棱柱的九条棱中随机选取两条, 则这两条棱所在直线至少有一条与直线 BD 异面的概率是()

已知函数 f(x) =tanx﹣ sinxcosx, 则()
