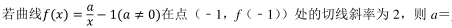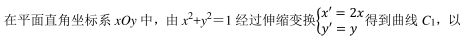
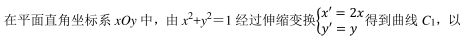
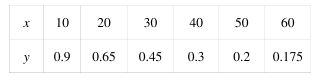
某茶场的黄金茶场市开发机构为了进一步开拓市场， 对黄金茶交易市场某个品种的黄金茶日销售情况进行调研， 得到这种黄金茶的定价 x（单位： 百元/kg） 和销售率 y（销售率是销售量与供应量的比值） 的统计数据如表：
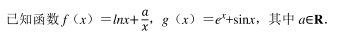
已知中心在坐标原点， 焦点在 x 轴上， 离心率为√5/5的椭圆 E， 满足其上、 下顶点和左、 右焦点构成的四边形的面积为 4．
（Ⅰ ） 求 E 的方程；
（Ⅱ ） 设 A， B 是 E 上的两点， 且满足 OA⊥OB（O 为坐标原点）， 试求△OAB 面积的最小值．
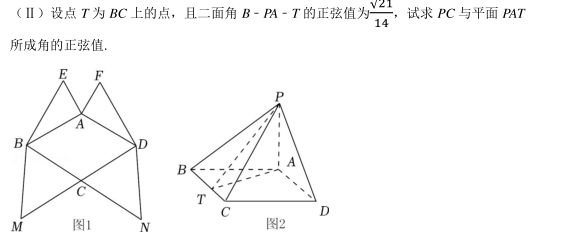
某商品的包装纸如图 1， 其中菱形 ABCD 的边长为 3， 且∠ABC＝60° ， AE＝AF= √3， BE＝DF＝2√3． 将包装纸各三角形沿菱形的边进行翻折后， 点 E， F， M， N汇聚为一点 P， 恰好形成如图 2 的四棱锥形的包裹．
（Ⅰ ） 证明： PA⊥底面 ABCD；
已知在各项均为正数的等差数列{a n }中， a 2 +a 3 +a 4 ＝21， 且 a 2 ﹣ 1， a 3 +1， a 4 +a 3构成等比数列{b n }的前三项．
（1） 求数列{a n }， {b n }的通项公式；
（2） 设数列{c n }＝____， 求数列{c n }的前 n 项和 S n ．
某高中学校需要安排男教师 x 名， 女教师 y 名做义工， x 和 y 需满足条件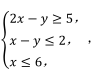
则该校安排教师最多为_________人
