已知中心在坐标原点， 焦点在 x 轴上， 离心率为√5/5的椭圆 E， 满足其上、 下顶点和左、 右焦点构成的四边形的面积为 4．
（Ⅰ ） 求 E 的方程；
（Ⅱ ） 设 A， B 是 E 上的两点， 且满足 OA⊥OB（O 为坐标原点）， 试求△OAB 面积的最小值．
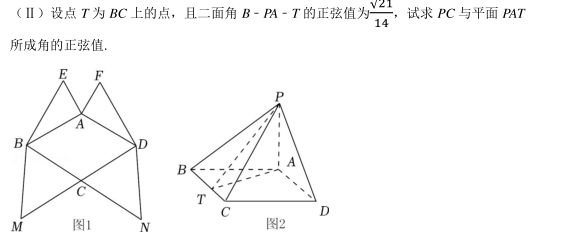
某商品的包装纸如图 1， 其中菱形 ABCD 的边长为 3， 且∠ABC＝60° ， AE＝AF= √3， BE＝DF＝2√3． 将包装纸各三角形沿菱形的边进行翻折后， 点 E， F， M， N汇聚为一点 P， 恰好形成如图 2 的四棱锥形的包裹．
（Ⅰ ） 证明： PA⊥底面 ABCD；
已知在各项均为正数的等差数列{a n }中， a 2 +a 3 +a 4 ＝21， 且 a 2 ﹣ 1， a 3 +1， a 4 +a 3构成等比数列{b n }的前三项．
（1） 求数列{a n }， {b n }的通项公式；
（2） 设数列{c n }＝____， 求数列{c n }的前 n 项和 S n ．
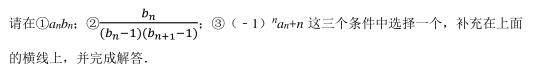
某高中学校需要安排男教师 x 名， 女教师 y 名做义工， x 和 y 需满足条件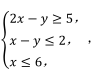
则该校安排教师最多为_________人
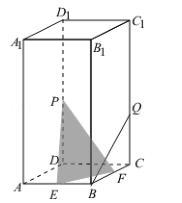
如图， 四棱柱 ABCD﹣ A 1 B 1 C 1 D 1 的底面是边长为 2 的正方形， 侧棱 AA 1 ⊥平面 ABCD，且 AA 1 ＝4， E、 F 分别是 AB、 BC 的中点， P 是线段 DD 1 上的一个动点（不含端点）， 过P、 E、 F的平面记为 α， Q 在 CC 1 上且 CQ＝1， 则下列说法正确的个数是（）
①三棱锥 C 1 ﹣ PAC 的体积是定值；
②当直线 BQ∥α 时， DP＝2；
③当 DP＝3 时， 平面 α 截棱柱所得多边形的周长为7√2；
④存在平面 α， 使得点 A 1 到平面 α 距离是 A 到平面 α 距离的两倍．
