如图， 四棱柱 ABCD﹣ A 1 B 1 C 1 D 1 的底面是边长为 2 的正方形， 侧棱 AA 1 ⊥平面 ABCD，且 AA 1 ＝4， E、 F 分别是 AB、 BC 的中点， P 是线段 DD 1 上的一个动点（不含端点）， 过P、 E、 F的平面记为 α， Q 在 CC 1 上且 CQ＝1， 则下列说法正确的个数是（）
①三棱锥 C 1 ﹣ PAC 的体积是定值；
②当直线 BQ∥α 时， DP＝2；
③当 DP＝3 时， 平面 α 截棱柱所得多边形的周长为7√2；
④存在平面 α， 使得点 A 1 到平面 α 距离是 A 到平面 α 距离的两倍．
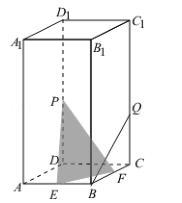
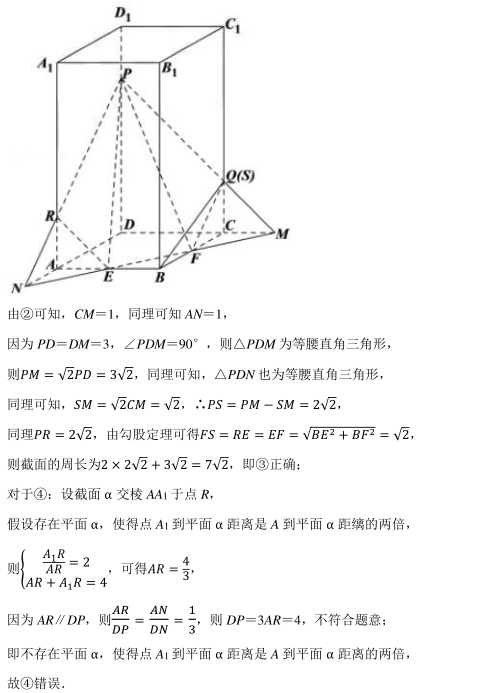
如图， 四棱柱 ABCD﹣ A 1 B 1 C 1 D 1 的底面是边长为 2 的正方形， 侧棱 AA 1 ⊥平面 ABCD，且 AA 1 ＝4， E、 F 分别是 AB、 BC 的中点， P 是线段 DD 1 上的一个动点（不含端点）， 过P、 E、 F的平面记为 α， Q 在 CC 1 上且 CQ＝1， 则下列说法正确的个数是（）
①三棱锥 C 1 ﹣ PAC 的体积是定值；
②当直线 BQ∥α 时， DP＝2；
③当 DP＝3 时， 平面 α 截棱柱所得多边形的周长为7√2；
④存在平面 α， 使得点 A 1 到平面 α 距离是 A 到平面 α 距离的两倍．
已知双曲线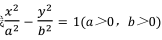
的左、 右焦点分别为 F 1 ， F 2 ， 点 A 是双曲线渐近线上一点， 且 AF 1 ⊥AO（其中 O 为坐标原点）， AF 1 交双曲线于点 B， 且|AB|＝|BF 1 |， 则双曲线的离心率为（）
北京 2022 年冬奥会即将开幕， 北京某大学 5 名同学报名到甲、 乙、 丙三个场馆做志愿者，每名同学只去 1 个场馆， 每个场馆至少安排 1 名志愿者， 则不同的安排方法共有（）
“牟合方盖” 是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体． 它由完全相同的四个曲面构成， 相对的两个曲面在同一个圆柱的侧面上， 好似两个扣合（牟合） 在一起的方形伞（方盖）． 其直观图如图， 图中四边形是为体现其直观性所作的辅助线． 当其主视图和侧视图完全相同时， 它的俯视图可能是（）
