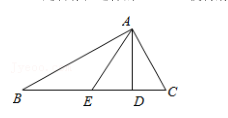
如图， 在△ABC 中， AB＞AC， AD、 AE 分别为 BC 边上的高和中线， AD＝4，DE＝3．
（1） 若∠BAC＝90° ， 求 AB 的长；
（2） 是否存在这样的△ABC， 使得射线 AE 和 AD 三等分∠BAC？
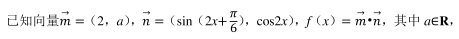
设函数 f（x） ＝﹣ x 2 +ax+b， 若不等式 f（x） ＞0 的解集为（﹣ 1， 3）．
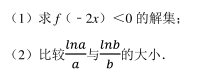
已知直线 y＝m 与函数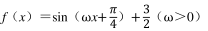
的图象相交， 若自左至右的三个相邻交点 A， B， C 满足 2|AB|＝|BC|， 则实数 m＝
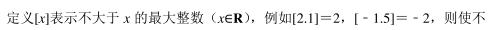
已知函数 f（x） ＝x 3 +ax 2 +bx+2 在 x＝1 处取得极小值 0， 若∀x 1 ∈[m， n]， ∃x 2 ∈[m，n]， 使得 f（x 1 ） ＝f（x 2 ）， 且 x 1 ≠x 2 ， 则 n﹣ m 的最大值为（）
