已知函数 f（x） ＝x 3 +ax 2 +bx+2 在 x＝1 处取得极小值 0， 若∀x 1 ∈[m， n]， ∃x 2 ∈[m，n]， 使得 f（x 1 ） ＝f（x 2 ）， 且 x 1 ≠x 2 ， 则 n﹣ m 的最大值为（）
已知函数 f（x） ＝x 3 +ax 2 +bx+2 在 x＝1 处取得极小值 0， 若∀x 1 ∈[m， n]， ∃x 2 ∈[m，n]， 使得 f（x 1 ） ＝f（x 2 ）， 且 x 1 ≠x 2 ， 则 n﹣ m 的最大值为（）
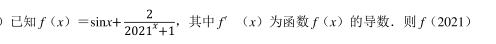
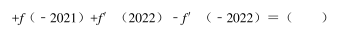
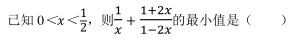
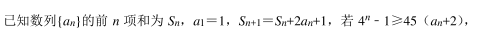则n的最小值是
已知命题 p：“∀x＞0， x+a﹣ 1≠0”， 命题 q：“∃x∈R， e x ﹣ ax＝0”， 若 p∧（￢q）为真命题， 则实数 a 的取值范围是（）
对于函数 f（x） ＝x2﹣ ax﹣ lnx（a∈R）， 下列说法正确的是（）
已知数列{an}是等差数列， Sn为其前 n 项和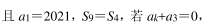
则k的值为
把函数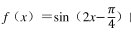
的图像上所有点的横坐标伸长为原来的 2 倍， 纵坐标保持不变， 再把所得的曲线向左平移 a（a＞0） 个单位长度， 得到函数 y＝cosx 的图像，则 a 可以是（）
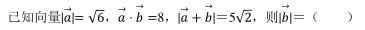
已知函数 f （x）＝log 2 |x﹣ a|的对称轴为直线 x＝2， 则函数 f （x+1）的对称轴为（）
