设某商品最大需求量为1200件,该商品的需求函数Q=Q(P),需求弹性η=P/(120-P)(η>0),P为单价(万元)。
(Ⅰ)求需求函数的表达式;
(Ⅱ)求P=100万元时的边际收益,并说明其经济意义。
(Ⅰ)根据弹性计算公式可得η=-(P/Q)(dQ/dP),即(P/Q)(dQ/dP)=P/(P-120),分离变量得dQ/Q=dP/(P-120),两边同时积分可得lnQ=ln(120-P)+C,得Q=C(120-P),由于最大需求量为1200,则Q(0)=1200,可得C=10。
所以需求函数的表达式为Q=10(120-P)=-10P+1200。
(Ⅱ)收益函数R的表达式为R=PQ=10(120-P)P=-10P2+1200P,边际收益函数dR/dQ=(dR/dP)(dP/dQ)=(-20P+1200)·(-1/10)=2P-120。
P=100万元时的边际收益为
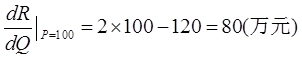
经济意义是当价格为100万元时,再多销售1单位产品增加的收益为80万元。