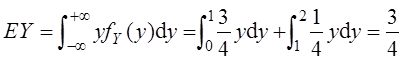设随机变量X的分布为P(X=1)=P(X=2)=1/2,在给定X=i的条件下,随机变量Y服从均匀分布U(0,i),i=1,2。
(Ⅰ)求Y的分布函数;
(Ⅱ)求期望E(Y)。
(Ⅰ)分布函数
F(y)=P(Y≤y)=P(Y≤y,X=1)+P(Y≤y,X=2)=P(Y≤y|X=1)P(X=1)+P(Y≤y|X=2)P(X=2)=0.5P(Y≤y|X=1)+0.5P(Y≤y|X=2)
当y<0时,F(y)=0;
当0≤y<1时,F(y)=y/2+(y/2)/2=3y/4;
当1≤y<2时,F(y)=1/2+(y/2)/2=y/4+1/2;
当y≥2时,F(y)=1。
故分布函数为
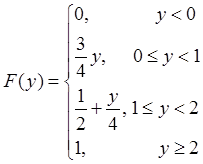
(Ⅱ)概率密度函数为
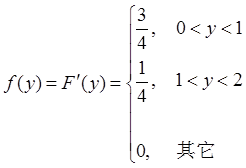
则