推荐等级:
发布时间: 2021-12-24 09:21
扫码用手机做题
设随机事件A,B相互独立,且P(B)=0.5,P(A-B)=0.3,则P(B-A)=( )。
本题解析:
由于事件A与事件B相互独立,则有P(A-B)=0.3=P(A)-P(AB)=P(A)-P(A)P(B)=P(A)-0.5P(A)=0.5P(A),故P(A)=0.6,P(B-A)=P(B)-P(AB)=0.5-0.5P(A)=0.2。

本题解析:
因为
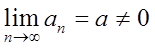
所以ε>0,N,当n>N时,有|an-a|<ε,即a-ε<an<a+ε,|a|-ε≤|an|≤|a|+ε,取ε=|a|/2,则知|an|>|a|/2。
设α1,α2,α3是三维向量,则对任意的常数k,l,向量组α1+kα3,α2+lα3线性无关是向量组α1,α2,α3线性无关的( )。
本题解析:
若向量组α1,α2,α3线性无关,则
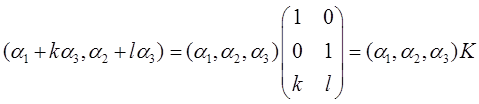
对任意的常数k,l,矩阵K的秩都等于2,所以向量α1+kα3,α2+lα3,一定线性无关。
当
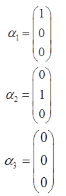
时,对任意的常数k,l,向量α1+kα3,α2+lα3,线性无关,但向量组α1,α2,α3线性相关。综上可得,向量组α1+kα3,α2+lα3线性无关是向量组α1,α2,α3线性无关的必要不充分条件。
设函数f(x)具有二阶导数,g(x)=f(0)(1-x)+f(1)x,则在区间[0,1]上( )。
本题解析:
方法一:若熟悉曲线在区间[a,b]上凹凸的定义,则可以直接做出判断,显然g(x)=f(0)(1-x)+f(1)x是连结(0,f(0))(1,f(1))两点的直线方程,故当f″(x)≥0时,曲线是凹的,即在区间[0,1]上f(x)≤g(x)。
方法二:若不熟悉曲线在区间[a,b]上凹凸的定义,则可令F(x)=f(x)-g(x)=f(x)-f(0)(1-x)-f(1)x,则F(0)=F(1)=0,且F″(x)=f″(x),故当f″(x)≥0时,曲线F(x)是凹的,从而F(x)≤F(0)=F(1)=0,即在区间[0,1]上F(x)=f(x)-g(x)≤0,即f(x)≤g(x)。
试卷分类:学硕教育学
练习次数:0次
试卷分类:学硕心理学
练习次数:0次
试卷分类:管理类联考综合
练习次数:0次
试卷分类:法硕非法学
练习次数:0次
试卷分类:法硕法学
练习次数:0次
试卷分类:西医综合
练习次数:0次
试卷分类:政治
练习次数:0次
试卷分类:中医综合
练习次数:0次
试卷分类:431金融学综合
练习次数:4次
试卷分类:431金融学综合
练习次数:7次