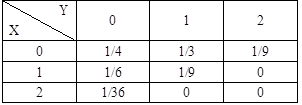袋中有1个红球、2个黑球与3个白球,现有放回地从袋中取两次,每次取一个球。以X,Y,Z分别表示两次取球所取得的红球、黑球与白球的个数。
(Ⅰ)求P{X=1|Z=0};
(Ⅱ)求二维随机变量(X,Y)的概率分布。
由于本题是有放回地取球,则基本事件总数为36。
(Ⅰ)P{X=1|Z=0}=P{X=1,Z=0}/P{Z=0}=[(1×2+2×1)/36]/[(3×3)/36]=4/9。
(Ⅱ)X,Y的可能取值均为0,1,2,且
P{X=0,Y=0}=(3×3)/36=1/4
P{X=0,Y=1}=(2×2×3)/36=1/3
P{X=0,Y=2}=(2×2)/36=1/9
P{X=1,Y=0}=(2×1×3)/36=1/6
P{X=1,Y=1}=(2×1×2)/36=1/9
P{X=1,Y=2}=0
P{X=2,Y=0}=(1×1)/36=1/36
P{X=2,Y=1}=0
P{X=2,Y=2}=0
故二维随机变量f(x,y)的概率分布如表1所示。
表1