2009年全国硕士研究生入学考试《数学三》真题

试卷预览

1 单选题 1分

设随机变量X与Y相互独立，且X服从标准正态分布N（0，1），Y的概率分布为P{Y＝0}＝P{Y＝1}＝1/2，记FZ（z）为随机变量Z＝XY的分布函数，则函数FZ（z）的间断点的个数为（　　）。

查看答案 开始考试

正确答案：B

本题解析：

FZ（z）＝P{Z≤z}＝P{XY≤z}＝P{XY≤z|Y＝0}P{Y＝0}＋P{XY≤z|Y＝1}P{Y＝1}＝P{0≤z}/2＋P{X≤z}/2。

当z≤0时，FZ（z）＝P{X≤z}/2＝ΦX（z）/2；当z＞0时，FZ（z）＝1/2＋P{X≤z}/2＝1/2＋ΦX（z）/2。于是

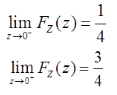
故z＝0为FZ（z）的间断点。

2 单选题 1分

设事件A与事件B互不相容，则（　　）。

查看答案 开始考试

正确答案：D

本题解析：

3 单选题 1分

查看答案 开始考试

正确答案：A

本题解析：

由题设可知

于是

4 单选题 1分

使不等式

成立的x的范围是（　　）。

查看答案 开始考试

正确答案：A

本题解析：

等价于

又在上述四个区间内，（1－sint）/t＞0，故若要使上式成立，则须0＜x＜1。

5 单选题 1分

当x→∞时，f（x）＝x－sinax与g（x）＝x2ln（1－bx）为等价无穷小，则（　　）。

查看答案 开始考试

正确答案：A

本题解析：

6 单选题 1分

查看答案 开始考试

正确答案：C

本题解析：

首先找出使f（x）无定义的点：即满足sinπx＝0的点，得x＝0，±1，±2，±3，…，若上述点为可去间断点，则f（x）在该点的左右极限存在且相等，又sinπx＝0，则必有分子x－x3＝0，即可去间断点可能为x＝0，±1。又

7 单选题 1分

查看答案 开始考试

正确答案：B

本题解析：

由于

因此选项B正确。

8 单选题 1分

设函数y＝f（x）在区间[－1，3]上的图形如图1所示。

说明:说明:11

则的图形为（　　）。

查看答案 开始考试

正确答案：D

本题解析：

由图可知：

（Ⅰ）在区间（－1，0）上，f（x）≥0，则F（x）在此区间单调递增，排除A项。

（Ⅱ）

表示y＝f（x），x＝0，x＝x0与x轴所围曲边梯形位于x轴上方的图形面积减去位于x轴下方的图形面积所得差值，则当0＜x＜1时，由图可知

排除C项。

（Ⅲ）又当2＜x＜3时，f（x）＝0，故

即F（x）在x＝2处连续，排除B项。