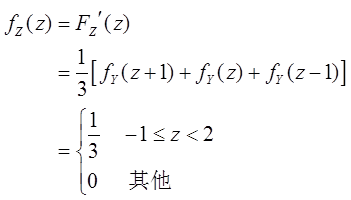设随机变量X与Y相互独立,X的概率分布为P{X=i}=1/3(i=-1,0,1),Y的概率密度为
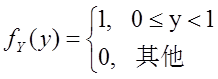
记Z=X+Y。
(Ⅰ)求P{Z≤1/2|X=0};
(Ⅱ)求Z的概率密度fZ(z)。
(Ⅰ)
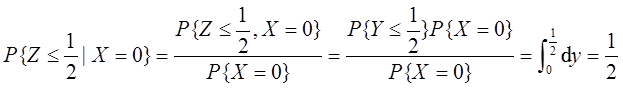
(Ⅱ)设Z的分布函数为F(z),则其值域非零时z的区间为[-1,2]。
当z<-1时,FZ(z)=0;
当z>2时,FZ(z)=1;
当-1≤z<2时,FZ(z)=P{Z≤z}=P{X+Y≤z}=P{X+Y≤z︱X=-1}P{X=-1}+P{X+Y≤z︱X=0}P{X=0}+P{X+Y≤z︱X=1}P{X=1}=[P{Y≤z+1}+P{Y≤z}+P{Y≤z-1}]/3=[FY(z+1)+FY(z)+FY(z-1)]/3。
故Z的分布密度函数为