研究者发现反应时间和错误率之间会存在一种制约性关系,人们将这种关系称为速度准确性权衡。下面的数据来自于一个反应时研究

根据表中数据,回答下面问题: (1)计算皮尔逊相关系数。 (2)皮尔逊相关计算的前提条件有哪些?假定上述数据不满足皮尔逊相关的条件,还可以通过什么方法考察反应时间和错误次数间的关系?试计算。
对题意进行分析,本题第一步考查皮尔逊积差相关系数的计算,第二步要求计算斯皮尔曼等级相关。皮尔逊相关的计算公式为

斯皮尔曼等级相关的计算公式,用等级差数法计算如下

因而,要计算这两种相关系数,需要先计算一些中间量。故先在下表中计算相关中间量。设反应时为变量X,错误次数为变量Y。

(1)将所计算的中间值代入皮尔逊相关公式,得
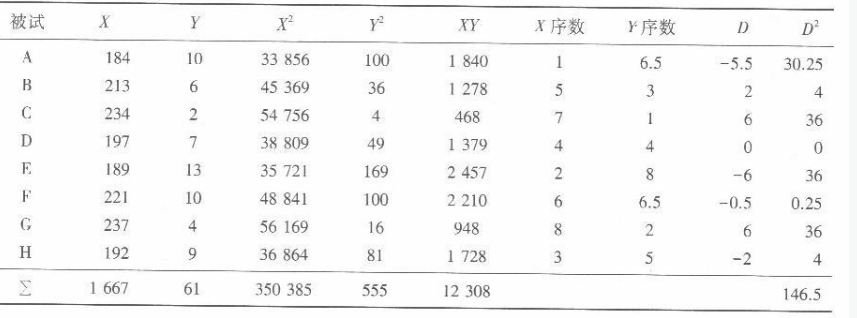
(2)计算皮尔逊积差相关的条件主要有四点,①数据是成对的;②两列变量各自总体的分布都是正态,即正态双变量;③两个相关的变量是连续变量;④两列变量之间的关系应是直线性的。如数据不符合皮尔逊积差相关的条件,还可以计算斯皮尔曼等级相关,过程如下:

因而,反应时间和错误次数的皮尔逊相关系数为-0.77,斯皮尔曼相关系数为-0.74。两者差异并不是很大。都表明反应时间和错误次数之间存在较高的负相关。相比皮尔逊相关,斯皮尔曼相关在样本量较少时计算相对简单,它对数据的分布形态也没有严格的要求。反之,皮尔逊积差相关则要求满足双变量正态分布的条件。但当数据同时满足两种相关系数的计算时,皮尔逊积差相关的精度更高。 本题主要考察皮尔逊相关和斯皮尔曼相关的计算方法及适用条件。两种相关系数在计算过程中,数据计算量比较大,学生在完成本题时应借助于科学计算器,会显著减少工作量。