一个研究者想要考察心理表象是否会影响记忆成绩,为此,他设计了一个实验。让两组独立的被试分别在有表象和无表象的条件之下学习一组40个名词,之后进行再认测验。下面是他所得到的结果:
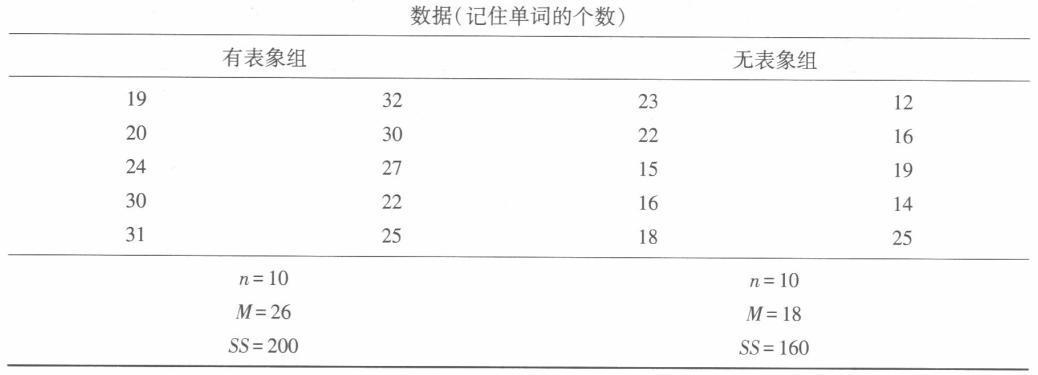
根据上述结果,回答问题: (1)该研究者能够得出心理表象影响记忆的结论吗?(α=0.05) (2)计算表象对于记忆影响的效应量(Cohen's d) (3)显著性检验和效应量的关系是什么?(t值表附后)
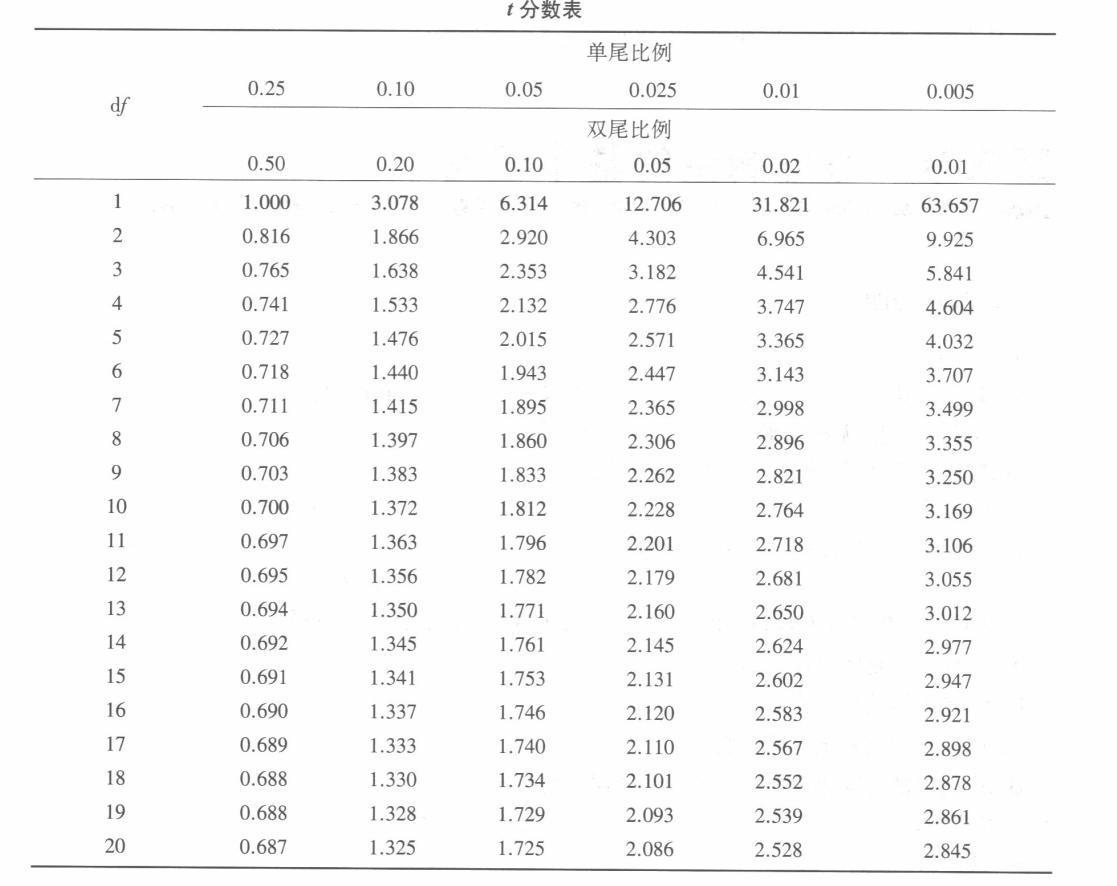
(l)根据题意,研究者是要考查有表象组和无表象组在再认测验成绩上是否有差异,因为总体方差未知,且样本量均小于30,可以认为两平均数之差的抽样分布符合£分布,适用的统计方法是独立样本t检验。检验步骤如下:①步骤1陈述假设 Ho:μ1-μ2=O(两组再认率没有差异,即表象没有效应) H1:μ1-μ2≠0(两组再认率有差异,表象有效应) 已知d=0. 05,由题意可知检验方向为双侧检验。 ②步骤2确定自由度及临界t分数 独立样本t检验,t分数的自由度为 df= df, +df2=(n1-l)+(n2-1)= 9+9= 18 查t分数表,可知在双尾检验下当自由度为18时,α=0.05双侧的t临界值为t=±2. 101。 ③步骤3计算检验统计量,即t值。 第一,计算两个样本的联合方差

第二,用联合方差来计算估计标准误
第三,计算t分数
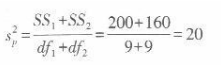
第四,作出判断。得到的t值(t=4.00)其绝对值大于前面查到的t的临界值,落入拒绝区上。因此,拒绝 H,并作出结论:用心理表象可以显著改变再认记忆成绩。 (2)效应大小指标Cohen's d的计算

(3)显著性检验和效应量的关系显著性考察的是样本中发现的效应是否能够推广到总体中去,而效应量指的是考察的效应本身的大小。显著性会受到样本容量的影响,当样本量很大时,很小的效应也会达到显著水平;另一方面,当效应量很大时,样本量较小时也能检验出该效应。 本题主要考查独立样本t检验,效应量指标Cohen's d的计算以及显著性检验和效应水平之间的关系。在实际研究过程中,不仅要关注显著性检验的结果,还必须关注考察的效应的大小,二者缺一不可。