根据下面的资料回答问题:

根据上述数据获得的期末成绩对期中成绩的回归方程为:Y= 24.5+0.723X。
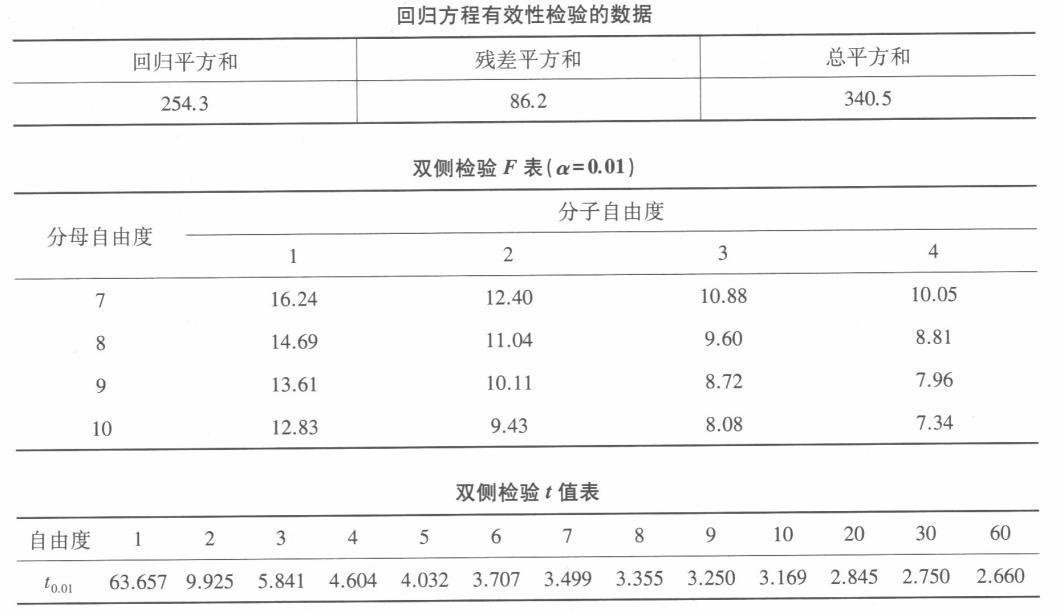
(1)对回归方程有效性进行检验。(2)期中考试得80分的学生,估计其期末考试得多少分?这一估计值的99%的置信区间是多少?
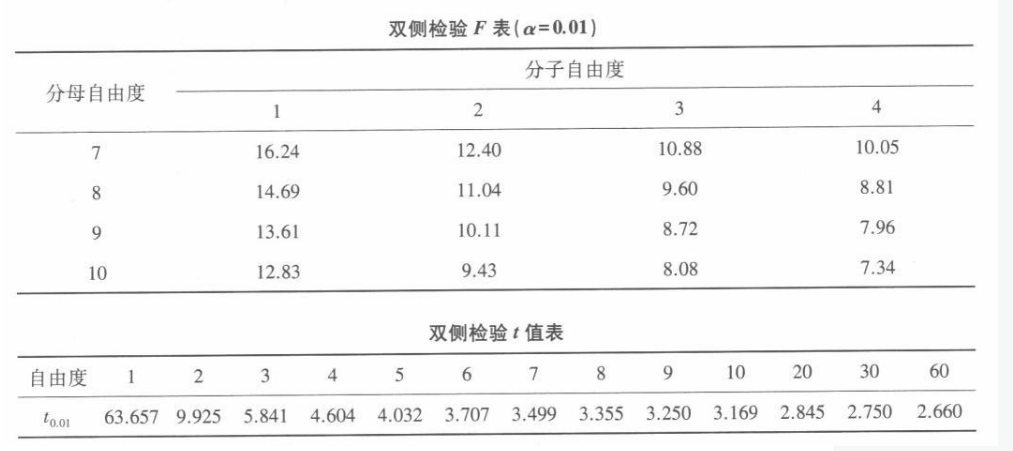
(1)对回归方程有效性进行检验①自由度的确定 总自由度:df=n一1=9 残差自由度:dfe= n-2=8 回归自由度:dfR= dft -dfe=1 ②均方的计算 回归均方:MSR =SSR/dfR= 254.3 残差均方:MSe= SSe/dfe= 10. 775 ③F检F=MSR/MSe= 23.6 查分子自由度为1,分母自由度为8的F分布表,得临界值Foo,(1,8)=14.69,23.6>14.69,因此所求回归方程有效。 (2)期中考试得80的估计成绩及估计成绩99%的置信区间 ①期中得80分的学生,期末得分的估计值由回归方程Y= 24.5+0.723X,将80分代入,进行计算得82.3。 ②估计值99%的置信区间第一步,求标准误,其公式为:

由此可知

故可知:
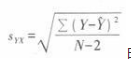
由此,SYX值就是MSE值的平方根,本题中即为10.775的平方根,等于3.283。第二步,查t表,t0.01(8)=3.355。第三步,y的99%的置信区间,[ 82. 3-3. 355x3. 283, 82. 3+3. 355x3. 283]即[71.29,93.31]. 回答本题的关键是要了解回归方程检验时自由度的确定以及估计的标准误的计算。