教师资格证考试《高中数学专业面试》真题汇编

试卷预览

1 问答题 1分

查看答案 开始考试

正确答案：

本题解析：

高中数学《终边相同的角》主要教学过程及板书设计

?? 教学过程

?? (一)创设情境、引入课题

?? 下面有两组简笔画，哪一组说明人一定过河了?

?? 第一组：

答辩题目解析

?? 1.函数零点判定定理与二分法求零点之间有什么关系?【专业知识问题】

?? 【参考答案】

?? 通过不断地把连续函数f(x)的零点所在的区间一分为二，使区间的端点逐步逼近零点，进而得到零点近似值的方法叫做二分法。由此可见，函数零点判定定理是二分法求零点的理论依据和前提。

?? 2.如果一个连续函数在定义域内是单调函数，那么函数的零点的个数可以确定吗?【专业知识问题】

【参考答案】

2 问答题 1分

查看答案 开始考试

正确答案：

本题解析：

3 问答题 1分

试讲题目：高中数学《直线与平面平行的判定定理》

3基本要求:

(1) 要有板书;

(2) 试讲十分钟左右;

(3) 条理清晰，重点突出;

(4)学生掌握直线与平面平行的判定定理。

答辩题目

1简单随机抽样的方法有哪些，为什么这些抽样方法统称为简单随机抽样?

2 课堂练习设置的原则是什么?

查看答案 开始考试

正确答案：

本题解析：

4 问答题 1分

试讲题目：高中数学《充分与必要条件》

3基本要求:

(1) 教学中注意师生间的交流互动，有适当的提问环节;

(2) 要求配合教学内容有适当的板书设计;

(3) 请在10分钟内完成试讲内容。

答辩题目

1充分与必要条件的定义是什么?

2教学过程中你主要设置了哪些问题，目的是什么?

查看答案 开始考试

正确答案：

本题解析：

5 问答题 1分

查看答案 开始考试

正确答案：

本题解析：

6 问答题 1分

查看答案 开始考试

正确答案：

本题解析：

7 问答题 1分

查看答案 开始考试

正确答案：

本题解析：

【教学过程】

(一)导入新课

问题1：我们已经知道角的度量单位是度、分、秒，它们的进率是60，角是否可以用其他单位度量呢?是否可以采用10进制?

问题2：角的弧度制是如何引入的?为什么要引入弧度制，好处是什么?角度制与弧度制的区别与联系?

(四)小结作业

小结：本节课你有哪些收获

作业：同桌互相给出角度或者弧度，另一个人进行转化

【板书设计】

【答辩题目解析】

1.弧度的定义是什么?

【参考答案】

所谓“弧度的定义”就是说，1弧度的角大小是怎样规定的? 我们知道“度”的定义是，“两条射线从圆心向圆周射出，形成一个夹角和夹角正对的一段弧。当这段弧长正好等于圆周长的360分之一时，两条射线的夹角的大小为1度。那么，弧度又是怎样定义的呢? 弧度的定义是：两条射线从圆心向圆周射出，形成一个夹角和夹角正对的一段弧。当这段弧长正好等于圆的半径时，两条射线的夹角大小为1弧度。比较一下，度和弧度的这两个定义非常相似。它们的区别，仅在于角所对的弧长大小不同。度的是等于圆周长的360分之一，而弧度的是等于半径。简单的说，弧度的定义是，当角所对的弧长等于半径时，角的大小为1弧度。

2.你本节课的教学目标是什么?

【参考答案】

【知识与技能】能正确进行角度与弧度的换算，熟记特殊角的弧度数。

【过程与方法】在合作探究的学习过程中，养成合理表述、科学抽象、规范总结的思维习惯，逐步在探索新知过程中锻炼推理的能力和数学知识的运用能力。

【情感态度价值观】进一步加强对辩证统一思想的理解，提高归纳概括总结能力，体会数学与生活的紧密联系。

8 问答题 1分

查看答案 开始考试

正确答案：

本题解析：

【教学过程】

(一)导入新课

提问：同学们，我们刚刚学习了基本事件的概念，那么什么是基本事件?基本事件又有什么特点呢?有没有人能举一个例子呢?

例1.列举出下列几个随机事件中的基本事件。

1.从a，b，c，d，中任取两个不同的字母的试验。

2.有五根细长的木棒，长度分别为1，3，5，7，9，任取三根。

3.掷两枚硬币，可能出现的结果。

(二)生成概念

提问：这三个例子有什么共同点?

通过学生自主探究，合作交流，师生共同归纳总结共同点，引出古典概型概念：

【答辩题目解析】

1.古典概型与几何概型的异同点?

【参考答案】

区别：古典概型的所有可能出现的基本事件个数为有限个;几何概型的所有可能出现的基本事件个数为无限个。

相同点：(1)每个基本事件出现的可能性一样;

(2)概率公式类似，都是事件所包含的基本事件的个数比上基本事件的总个数。

2.本节课的教学目标是什么?

【参考答案】

【知识与技能】

会判断古典概型，会用列举法计算一些随机事件所含的基本事件数和试验中基本事件的总数;能够利用概率公式求解一些简单的古典概型的概率。

【过程与方法】

通过从实际问题中抽象出数学模型的过程，提升从具体到抽象从特殊到一般的分析问题的能力。

【情感态度与价值观】

增加学生合作学习交流的机会，在体会概率意义的同时，感受与他人合作的重要性以及初步形成实事求是地科学态度和锲而不舍的求学精神。

9 问答题 1分

查看答案 开始考试

正确答案：

本题解析：

【教学过程】

2.请对学生情况进行分析?

【参考答案】

圆的方程是学生在初中学习了圆的概念和基本性质后，又掌握了求曲线方程的一般方法的基础上进行研究的。但由于学生学习解析几何的时间还不长、学习程度较浅，且对坐标法的运用还不够熟练，在学习过程中难免会出现困难。另外学生在探究问题的能力，合作交流的意识等方面有待加强。

10 问答题 1分

1.题目：直线与平面垂直的判定

2.内容：

3.基本要求：

（1）试讲时间10分钟左右；

（2）讲解要目的明确、条理清楚、重点突出；

（3）根据讲解的需要适当板书和作图；

（4）呈现探究直线与平面垂直的判定定理的过程；

（5）说明应用直线与平面垂直的判定定理的条件。

答辩题目：1.判断直线与平面垂直的方法有哪些?

2.直线与平面平行的判定定理是什么?如何推导出来的?

查看答案 开始考试

正确答案：

本题解析：

【教学过程】

(一)引入新课

直接阐述生活中有很多直线和平面垂直的现象，直接引出本节课的学习内容《直线与平面垂直的判定》。

(二)探索新知

1.直线与平面垂直的概念

图片展示旗杆与地面、大桥的桥柱与水面的图片。

提问：通过对这些现象的观察，说一说旗杆与地面、大桥的桥柱与水面给大家的直观感受是什么?再说一说生活中还有哪些直线与平面垂直的现象?

预设：图片中旗杆与地面、大桥的桥柱与水面给人垂直的现象。

教室中的桌腿和地面、两面墙相交的直线与地面……

展示将旗杆与地面抽象成数学图形。

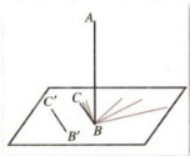
讲解图形随时间的变化而变化，但是旗杆AB所在直线与BC所在直线一直垂直。

直线与平面垂直的概念:如果直线l与平面a内的任意一条直线都垂直,我们就说直线l与平面a互相垂直,记作l⊥a。直线l叫做平面a的垂线，平面a叫做直线l的垂面，直线与平面垂直时，它们唯一的公共点p叫做垂足。

强调:一条直线与一个平面垂直,这条直线垂直于这个平面内的任意一条直线。

追问:如果一条直线垂直于一个平面内的无数条直线,那么这条直线是否与这个平面垂直?

组织学生同桌探究。

总结：这些无数条的直线必须有相交直线。

2.直线与平面垂直的判定

探究:如图所示,请同学们准备一块三角形的纸片，我们一起来做一个实验：过△ABC的顶点A翻折纸片，得到折痕AD,将翻折后的紙片竖起放置在桌面上(BD,DC与桌面接触)。

(1)折痕AD与桌面垂直吗?

(2)如何翻折才能使折痕AD与桌面所在平面a垂直?

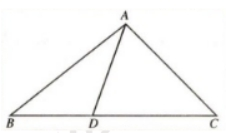
教师根据学生回答总结:AD垂直BC时,AD所在直线与桌面所在平面a垂直

追问:1.折痕AD所在直线与桌面所在平面a上的一条直线垂直,就可以判断AD垂直平面a。你同意他的说法吗?

2.如图所示,由折痕AD⊥BC,翻折之后垂直关系不变,即AD⊥CD,AD⊥BD。由此你能得到什么结论?

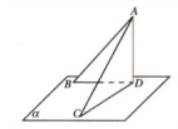
师生共同总结:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。

(三)课堂练习

例1:如图所示,已知a∥b,a⊥a,求证b⊥a。

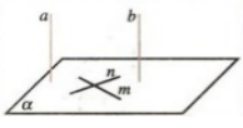
(四)小结作业

提问:本节课你学会了什么?

引导学生回顾:直线与平面垂直的概念与判定。

课后作业:练习1、2题。