2011全国硕士研究生入学考试《数学2》真题

试卷预览

1 单选题 1分

设A＝（α1，α2，α3，α4）是4阶矩阵，A*为A的伴随矩阵。若（1，0，1，0）T是方程组Ax＝0的一个基础解系，则A*x＝0的基础解系可为（　　）。

查看答案 开始考试

正确答案：D

本题解析：

因为Ax＝0基础解系含一个线性无关的解向量，所以r（A）＝3，于是r（A*）＝1，故A*x＝0基础解系含3个线性无关的解向量。又A*A＝|A|E＝0且r（A）＝3，所以A的列向量组中含A*x＝0的基础解系。

因为（1，0，1，0）T是方程组Ax＝0的基础解系，所以α1＋α3＝0，故α1，α2，α4或α2，α3，α4线性无关，显然α2，α3，α4为A*x＝0的一个基础解系，故选D项。

2 单选题 1分

设A为3阶矩阵，将A的第2列加到第1列得矩阵B，再交换B的第2行与第3行得单位矩阵。记

则A＝（　　）。

查看答案 开始考试

正确答案：D

本题解析：

3 单选题 1分

查看答案 开始考试

正确答案：C

本题解析：

4 单选题 1分

设函数f（x）在x＝0处可导，且f（0）＝0，则（　　）。

查看答案 开始考试

正确答案：B

本题解析：

5 单选题 1分

设函数f（x），g（x）均有二阶连续导数，满足f（0）＞0，g（0）＜0，f′（0）＝g′（0）＝0，则函数z＝f（x）g（y）在点（0，0）处取得极小值的一个充分条件是（　　）。

查看答案 开始考试

正确答案：A

本题解析：

由z＝f（x）g（y）得

?z/?x＝f′（x）g（y）

?z/?y＝f（x）g′（y）

B＝?2z/?x?y＝f′（x）g′（y）

A＝?2z/?x2＝f″（x）g（y）

C＝?2z/?y2＝f（x）g″（y）

在（0，0）点，A＝f″（0）g（0），B＝f′（0）g′（0）＝0，C＝f（0）g″（0）。由

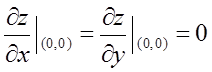
可得，（0，0）是z＝f（x）g（y）可能的极值点。若z＝f（x）g（y）在（0，0）有极小值。由AC－B2＞0且A＞0?f″（0）＜0，g″（0）＞0故选A项。

6 单选题 1分

函数f（x）＝ln|（x－1）（x－2）（x－3）|的驻点个数为（　　）。

查看答案 开始考试

正确答案：C

本题解析：

7 单选题 1分

已知当x→0时，函数f（x）＝3sinx－sin3x与cxk是等价无穷小，则（　　）。

查看答案 开始考试

正确答案：C

本题解析：

因为

所以f（x）＝4x3＋ο（x3）～4x3，于是c＝4，k＝3，故选C项。

8 单选题 1分

设

则I，J，K的大小关系为（　　）。

查看答案 开始考试

正确答案：B

本题解析：

x∈（0，π/4），有sinx＜cosx＜1＜cotx，则lnsinx＜lncosx＜0＜lncotx，故

即I＜K＜J，故选B项。