推荐等级:
发布时间: 2021-12-30 16:23
扫码用手机做题
设函数f(x)在(-∞,+∞)内连续,其导函数的图形如图1所示,则( )。
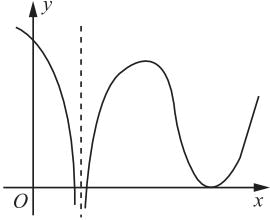
本题解析:
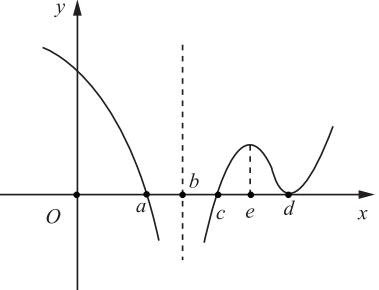
如图2所示,f′(x)在a,c,d三点取值为0,有可能为f(x)的极值点。a点:当x<a时,f′(x)>0;当x>a时,f′(x)<0,所以a点为极大值点。c点:当x<c时,f′(x)<0;当x>c时,f′(x)>0,所以c点为极小值点。d点:当x<d时,f′(x)>0;当x>d时,f′(x)>0,所以d点不是极值点。所以f(x)有2个极值点。
图中,b,e,d有可能为f(x)的拐点。b点:当x<b时,f′(x)递减,f″(x)<0;当b<x<e时,f′(x)递增,f″(x)>0所以b点为拐点。e点:当b<x<e时,f′(x)递增,f″(x)>0;当e<x<d时,f′(x)递减,f″(x)<0,所以e点为拐点。d点:当e<x<d时,f′(x)递减,f″(x)<0,当x>d时,f′(x)递增,f″(x)>0,所以d点为拐点。所以f(x)有3个拐点。
设函数fi(x)(i=1,2)具有二阶连续导数,且fi″(x0)<0(i=1,2),若两条曲线y=fi(x)(i=1,2)在点(x0,y0)处具有公切线y=g(x),且在该点处曲线y=f1(x)的曲率大于曲线y=f2(x)的曲率,则在x0的某个邻域内,有( )。
本题解析:
由题可知,f1(x0)=f2(x0)=g(x0),f1′(x0)=f2′(x0)=g′(x0),且根据曲率大小关系有f1″(x0)<f2″(x0),g″(x0)=0。
令F(x)=f1(x)-f2(x),则F(x0)=0,F′(x0)=f1′(x0)-f2′(x0)=0,F″(x0)=f1″(x0)-f1″(x0)<0。所以,F(x0)=0为F(x)的一个极大值,即在x0的某个邻域内F(x)≤0,也即f1(x)≤f2(x)。
同理设G(x)=fi(x)-g(x)(i=1,2),可得在x0的某个邻域内G(x)≤0,也即fi(x)≤g(x)。
综上,在x0的某个邻域内,f1(x)≤f2(x)≤g(x)。
试卷分类:学硕教育学
练习次数:0次
试卷分类:学硕心理学
练习次数:0次
试卷分类:管理类联考综合
练习次数:0次
试卷分类:法硕非法学
练习次数:0次
试卷分类:法硕法学
练习次数:0次
试卷分类:西医综合
练习次数:0次
试卷分类:政治
练习次数:0次
试卷分类:中医综合
练习次数:0次
试卷分类:431金融学综合
练习次数:4次
试卷分类:431金融学综合
练习次数:7次