教学设计。
《义务教育数学课程标准(2011年版)》在课程内容中要求:创新意识的培养是现代数学教育的根本任务,应体现在数学教与学的过程之中,学生自己发现问题和提出问题是创新的基础;独立思考、学会思考是创新的核心;归纳概括得到猜想和规律,并加以验证是创新的重要方法。
素材:如图所示,将正方形纸片ABCD折叠,使B点落在CD边上一点E(不与C,D重合),压平后得到折痕删。
(1)试根据点E在CD上的位置变化,设置适当条件,编制一道数学题目;(不要求解答)
(2)依据上述素材和要求,试以提出问题为主线进行“探究式”解题教学,撰写一份培养学生观察与发现,归纳与推理能力的教学过程设计。(只需写出教学过程,突出探究的方法与问题即可)
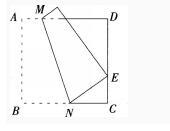
(1)本题具有开放性,题目设置合理即可,下面是几个示例: 设正方形纸片ABCD边长为2,
 (2)导入:
(2)导入:
采用练习导人法.利用一个简单的练习题引入本节课内容。
新课讲授:
根据导入的例题,提出问题:在之前学习的三角形知识中,有哪些常用的性质和定理?
预设:①全等三角形判定定理,②相似三角形判定定理,③等腰三角形性质,④勾股定理……
找学生回答并追问,明确具体的性质和定理内容。
在复习之前的知识之后,结合(1)中②③进行“探究式”解题教学。
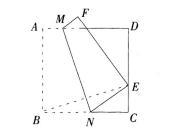
给出例题:如图所示,已知正方形纸片ABCD边长为2,将正方形纸片ABCD折叠,使曰点落在CD边上一点E(不与C,D重合),压平后得到折痕MN,A点落在点F处。
问题1:根据条件,能够获得哪些结论?
学生七嘴八舌地说着,教师提问后总结

问题6:求E在什么位置时,△ENC的面积取得最大值?
之前的几个问题都是为了解决问题6做铺垫的,在前五个问题的基础上研究问题6,几何问题已经转化成函数求最值问题.即求函数 的最大值。
计算部分留给学生。教师对本节课做小结:同学们,我们在学习数学的过程中要善于独立思考,学会在已知条件的基础上归纳概括得出猜想和规律,发现问题、提出问题并想办法去解决问题。要大胆的去尝试,把看起来难的问题。细化成若干个可以解决的小问题,在不断探究不断深入的过程中就会自然而然地解决问题。
作业:已知正方形ABCD边长为2,将正方形纸片ABCD折叠,使B点落在CD边上一点E(不与C,D重合),

我国保护少年儿童权益的专项法律是《中华人民共和国未成年人保护法》。( )
MP3( )。
计算机软件是指( )。
下面哪一项不属于维护交易安全原则的内容?( )
围绕《建国以来的重大科技成就》一课,做一个教案。
请围绕“城乡发展一体化”写一篇小论文,题目自拟,角度不限,要求:结构完善、条理清晰、有说服力。
在国际关系中,第三世界国家历来是中国团结合作的对象,因为 ①第三世界国家是国际社会一支重要的政治力量 ②团结第三世界国家符合中国的国家利益 ③合作是第三世界国家共同发展的必由之路 ④第三世界国家在南北关系中处于主导地位( )
微观经济学要解决的问题是( )
机关文书部门或业务部门在年终或第二年上半年对归卷的文件材料进行整理等工作,称为( )。
20世纪70年代中国外交有了重大突破和转机,转变的关键是( )