设函数y=f(x)在(-∞,+∞)内连续,其导函数的图形如图1所示,则( )。
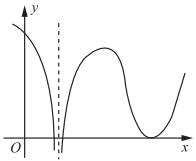
如图2所示,f′(x)在a,c,d三点取值为0,有可能为f(x)的极值点。a点:当x<a时,f′(x)>0;当x>a时,f′(x)<0,所以a点为极大值点。c点:当x<c时,f′(x)<0;当x>c时,f′(x)>0,所以c点为极小值点。d点:当x<d时,f′(x)>0;当x>d时,f′(x)>0,所以d点不是极值点。所以,f(x)有2个极值点。
图2中,b,e,d有可能为f(x)的拐点。b点:当x<b时,f′(x)递减,f″(x)<0;当b<x<e时,f′(x)递增,f″(x)>0,所以b点为拐点。e点:当b<x<e时,f′(x)递增,f″(x)>0;当e<x<d时,f′(x)递减,f″(x)<0,所以e点为拐点。d点:当e<x<d时,f′(x)递减,f″(x)<0;当x>d时,f′(x)递增,f″(x)>0,所以d点为拐点。所以,f(x)有3个拐点。
