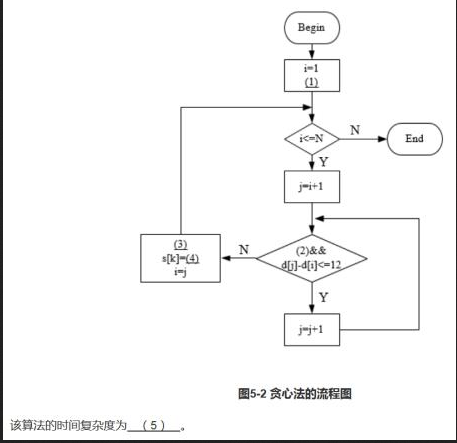
(1 )k=0
(2) J<=N
(3) k=k+1或k++ ,或者其他等价形式
(4) d[i]+6 ,或者其他等价形式
(5)0(N)
该题是一个应用型的算法分析题,主要考查考生对贪心算法的理解以及对程序流程图的掌握;做题的关键是对分析清楚题意,并明确流程图中的贪心条件。
该题可转化为求解能覆盖所有房子的基站部署方案的问题,即通过一系列选择求最优解的问题。不难发现,该问题具有最优子结构,并且具有贪心选择性质,可以用贪心法来求解。
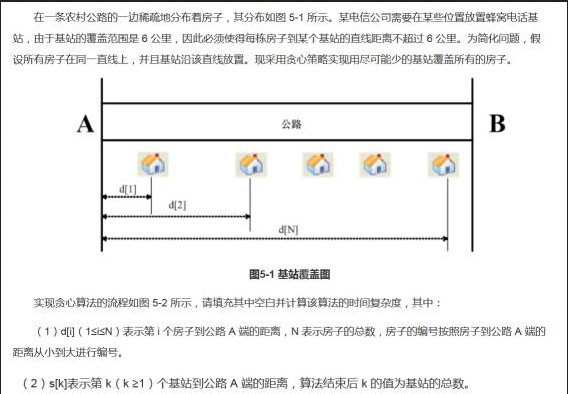
贪心法是一种不求最优解,只求满意解的算法。首先初始化, k=0 ;若两房间的距离不超过12公立,则不建基站。否则建基站。算法思想:问题的规模为N。从第一个房子 (最左端)开始部署基站.把第一个基站放置在该房子右方的6公里处,这时,该基站会覆盖从第一个房子到其右方12公里的直线的长度上的所有房子。假设覆盖了N:个房子。此时问题规模编程了N-N1。把第一个基站覆 盖的房子去掉,再从N-N;中选择第一个 (最左端)房子开始布局基站,将第二个基站放置在该房子右方的6公里处。以此类推,直至所有的房子被覆盖。在该算法中包含两个循环,但实际上只是遍历所有房子次,所以算法的时间复杂度为0(N)。


阅读下列说明和C++代码,将应填入( )处的字句写在答题纸的对应栏内。
【说明】
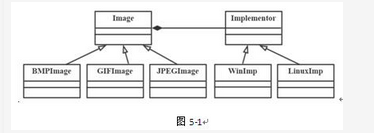
某图像预览程序要求能够查看BMP、JPEG和GIF三种格式的文件,且能够Windows和Linux两种操作系统上运行。程序需具有较好的扩展性以支持新的文件格式和操作系统。为满足上述需求并减少所需生成的子类数目,现采用桥接(Bridge)模式进行设计,得到如图5-1所示的类图。
【c++代码】
#include
#include
using namespace std;
class matrix{//各种格式的文件最终都被转化为像素矩阵
//此处代码省略
};
class implement{
public:
(1) ;//显示像素矩阵m
};
class winimp:public implementor{
public:
void dopaint(matrix m){/*调用windows系统的绘制函数绘制像素矩阵*/}
};
class linuximp: public implementor{
public:
void dopaint(matrix m){/*调用linux系统的绘制函数绘制像素矩阵*/}
};
class imag{
public:
void setimp(implementor *imp){this.imp=imp;}
virtual void parsefile(string filename)=0;
protected:
implenentor *imp;
};
class bmpimage:public image{
//此处代码省略
};
class gifimage:public image{
public:
void parsefile(string filename){
//此处解析gif文件并获取一个像素矩阵对象m
(2) ;//显示像素矩阵m
}
};
class jpegimage:public image{
//此处代码省略
};
int main(){
public static void main(string[] args){
//在linux操作系统上查看demo.gif图像文件
imag imag= (3) ;
implementor imageimp= (4) ;
(5) ;
image.parsefile(“demo.gif”);
}
}
某咖啡店售卖咖啡时,可以根据顾客的要求在其中加入各种配料,咖啡店会根据所加入的配料来计算费用。咖啡店所供应的咖啡及配料的种类和价格如下表所示。
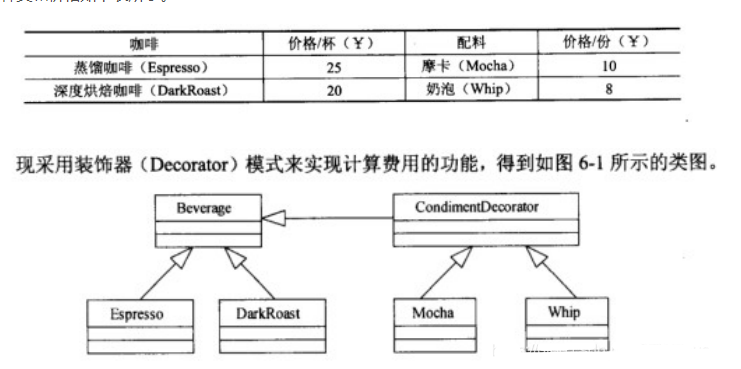


阅读下列说明和C代码,回答问题1至问题2,将解答写在答题纸的对应栏内。
【说明】
一个无向连通图G点上的哈密尔顿(Hamiltion)回路是指从图G上的某个顶点出发,经过图上所有其他顶点一次且仅一次,最后回到该顶点的路径。哈密尔顿回路算法的基础如下:假设图G存在一个从顶点V0出发的哈密尔顿回路V1--V2--V3--...--Vn-1--V0。算法从顶点V0出发,访问该顶点的一个未被访问的邻接顶点V1,接着从顶点V1出发,访问V1一个未被访问的邻接顶点V2,..。;对顶点Vi,重复进行以下操作:访问Vi的一个未被访问的邻接接点Vi+1;若Vi的所有邻接顶点均已被访问,则返回到顶点Vi-1,考虑Vi-1的下一个未被访问的邻接顶点,仍记为Vi;直到找到一条哈密尔顿回路或者找不到哈密尔顿回路,算法结束。
【C代码】
下面是算法的C语言实现。
(1)常量和变量说明
n :图G中的顶点数
c[][]:图G的邻接矩阵
K:统计变量,当前已经访问的顶点数为k+1
x[k]:第k个访问的顶点编号,从0开始
Visited[x[k]]:第k个顶点的访问标志,0表示未访问,1表示已访问
(2)C程序
#include
#include
#define MAX 100
void Hamilton(int n,int x[MAX] , int c[MAX][MAX]){
int i;
int visited[MAX];
int k;
/*初始化x数组和visited数组*/
for (i=0:i x[i]=0; visited [i]=0; } /*访问起始顶点*/ k=0 (1); x[0]=0 ; k=k+1 ; /*访问其他顶点*/ while(k>=0){ x[k]=x[k]+1; while(x[k] if ((2)&& c [x[k-1]] [x[k]] ==1){/*邻接顶点x[k]未被访问过*/ break; }else{ x[k] = x[k] +1 } } if(x[k] for (k=0;k printf(〝%d--〝,x[k] ) ; /*输出哈密尔顿回路*/ } printf(〝%d\n〝,x[0] ) ; return; }else if (x[k] (4) k=k+1; }else{/*没有未被访问过的邻接顶点,回退到上一个顶点*/ x[k]=0; visited [x[k]]=0; (5); } } } 【问题1】(10分) 根据题干说明。填充C代码中的空(1)~(5)。 【问题2】(5分) 根据题干说明和C代码,算法采用的设计策略为( ),该方法在遍历图的顶点时,采用的 是( )方法(深度优先或广度优先)。
阅读以下说明和C程序,将应填入 (n) 处的字句写在对应栏内。[说明]
下面的程序用Dole Rob算法生成N阶(N为奇数)魔方阵(各行、列、对角线数字之和相等)。该算法的过程为:从1开始,按如下方法依次插入各自然数,直到N2为止。
①在第一行的正中插入1。
②新位置应当处于最近插入位置的右上方,若该位置已超出方阵的上边界,则新位置取应选列的最下一个位置;若超出右边界,则新位置取应选行的最左一个位置。
③若最近插入的元素是N的整数倍,则选同列的下一行位置为新位置。
例如,3阶魔方阵如下所示:
8 1 6
3 5 7
4 9 2
[C程序]
include<stdio.h>
include<stdlib.h>
define SIZE 50
main()
{
int row, col, n, value;
int a[SIZE+1][SIZE+1]; /*不使用下标为0的元素*/
printf("请输入要输出魔方阵的阶数n(奇数, <%d):n=", SIZE);
scanf("%d", &n);
if(!(n%2) || n<1 || (1) ){
printf("输入数据有误!\n");
exit(0);
}
row=1; col=(n+1)/2; value=1;
while(value<= (2) ) {
a[row][col]=value;
/*计算下一位置*/
if(value%n!=0){
row--; (3) ;
if(row<1)row=n;
if(col>n) (4) ;
}
else row++;
value= (5) ;
}
printf("\n%d阶魔方阵如下所示:\n\n", n);
for(row=1; row<=n; row++){
for(col=1; col<=n; col++)
printf("%5d", a[row][col]);
printf("\n");
}
}
阅读下列说明和Java代码,将应填入( )处的字句写在答题纸的对应栏内。
【说明】
某图像预览程序要求能够查看BMP、JPEG和GIF三种格式的文件,且能够在Windows和Linux两种操作系统上运行。程序需具有较好的扩展性以支持新的文件格式和操作系统。为满足上述需求并减少所需生成的子类数目,现采用桥接模式进行设计,得到如图6-1所示的类图。
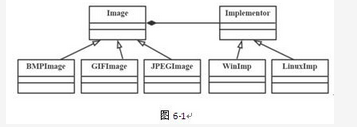
【Jave代码】
【Jave代码】
Import java.util.*;
class Matrix{ //各种格式的文件最终都被转化为像素矩阵
//此处代码省略
};
abstract class Implementor{
Public(1);//显示像素矩阵 m
};
class WinImp extends Implementor{
public void doPaint(Matrix m){ //调用 Windows 系统的绘制函数绘制像素矩阵
}
};
class LinuxImp extends Implementor{
public void doPaint(Matrix m){ //调用 Linux 系统的绘制函数绘制像素矩阵
}
};
abstract class Image{
public void setImp(Implementor imp){ this.imp= imp; }
public abstract void parseFile(String fileName);
protected Implementor imp;
};
class BMPImage extends Image{
//此处代码省略
};
class GIFImage extends Image{
public void parseFile(String fileName) {
//此处解析BMP文件并获得一个像素矩阵对象m
(2);//显示像素矩阵m
}
};
Class Main{
Public static viod main(String[]args){
//在Linux操作系统上查看demo.gif图像文件
Image image=(3)
Implementor imageImp=(4)
(5)
Image.parseFile(〝demo.gif〝);
}
}
阅读下列说明和Java代码,回答问题,将解答填入答题纸的对应栏内。
【说明】
某灯具厂商欲生产一个灯具遥控器,该遥控器具有7个可编程的插槽,每个插槽都有开关按钮,对应着一个不同的灯。利用该遥控器能够统一控制房间中该厂商所有品牌灯具的开关,现采用Command(命令)模式实现该遥控器的软件部分。Command模式的类图如下图所示。
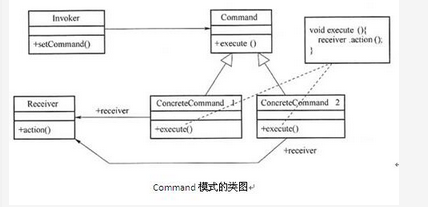
【Java代码】
【Java代码】
class Light {
public Light() {}
public Light(String name) { /* 代码省略 */ }
public void on() { /* 代码省略 */ } // 开灯
public void off() { /* 代码省略 */ } // 关灯
// 其余代码省略
}
(1) {
public void execute();
}
class LightOnCommand implements Command { // 开灯命令
Light light;
public LightOnCommand(Light light) { this.light=light; }
public void execute() { (2) ; }
}
class LightOffCommand implements Command { // 关灯命令
Light light;
public LightOffCommand(Light light) { this.light=light; }
public void execute(){ (3) ; }
}
class RemoteControl { // 遥控器
Command[] onCommands=new Command[7];
Command[] offCommands=new Command[7];
public RemoteControl() { /* 代码省略 */ }
public void setCommand(int slot, Command onCommand, Command offCommand) {
(4) =onCommand;
(5) =offCommand;
}
public void onButtonWasPushed(int slot) {
(6) ;
}
public void offlButtonWasPushed(int slot){
(7) ;
}
}
class RemoteLoader {
public static void main(String[] args) {
RemoteControl remoteControl=new RemoteControl();
Light livingRoomLight=new Light("Living Room");
Light kitchenLight=new Light("kitchen");
LightOnCommand livingRoomLightOn=new LightOnCommand(livingRoomLight);
LightOffCommand livingRoomLightOff=new LightOffCommand(livingRoomLight);
LightOnCommand kitchenLightOn=new LightOnCommand(kitchenLight);
LightOffCommand kitchenLightOff=new LightOffCommand(kitchenLight);
remoteControl.setCommand(0, livingRoomLightOn, livingRoomLightOff);
remoteControl.setCommand(1, kitchenLightOn, kitchenLightOff);
remoteControl.onButtonWasPushed(0);
remoteControl.offButtonWasPushed(0);
remoteControl.onButtonWasPushed(1);
remoteControl.offButtonWasPushed(1);
}
}
阅读以下说明和C程序,将应填入(n)处的字句写在对应栏内。
【说明】
下面的程序按照以下规则输出给定名词的复数形式。
a.若名词以“y”结尾,则删除y并添加“ies”;
b.若名词以“s”、“ch”或“sh”结尾,则添加“es”;
c.其他所有情况,直接添加“s”。
【C程序】
include <stdio.h>
include <string.h>
char*plural(char *word)
{
int n;
char *pstr;
n=strlen(word); /*求给定单词的长度*/
pstr=(char*)malloc(n+3);/*申请给定单词的复数形式存储空间*/
if (!pstr||n<2)
return NULL;
strcpy(pstr,word); /*复制给定单词*/
if ((1))
{
pstr[n-1]='i';pstr[n] ='e';pstr[n+1]='s';(2);
}
else
if(pstr[n-1]=='s'| |pstr[n-1]=='h'&&((3)))
{
pstr[n]='e';pstr[n+1]='s';pstr[n+2]='/0';
}
else
{ pstr[n]='s';pstr[n+1]='/0';)
(4);
}
main()
{ int i; char *ps;
char wc[9][10]=
{'chair','dairy','boss','circus','fly','dog','church','clue','dish');
for(i = 0;i<9; i++) {
ps= (5) ;
printf('%s: %s/n',wc[i],ps); /*输出单词及其复数形式*/
free(ps); /*释放空间*/
}
system('pause');
}
阅读下列说明和C代码,回答问题,将解答填入答题纸的对应栏内。
【说明】
计算一个整数数组a的最长递增子序列长度的方法描述如下:
假设数组a的长度为n,用数组b的元素b[i]记录以a[i](0≤i<n)为结尾元素的最长递增子序列的长度为 ;其中b[i]满足最优子结构,可递归定义为:
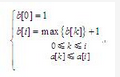
【C代码】
下面是算法的C语言实现。
(1)常量和变量说明
a:长度为n的整数数组,待求其最长递增子序列
b:长度为n的数组,b[i]记录以a[i](0≤i<n)为结尾元素的最长递增子序列的长度,其中0≤i<n
len:最长递增子序列的长度
i, j:循环变量
temp:临时变量
(2)C程序
#include
int maxL(int*b, int n) {
int i, temp=0;
for(i=0; i if(b[i]>temp) temp=b[i]; } return temp; } int main() { int n, a[100], b[100], i, j, len; scanf("%d", &n); for(i=0; i scanf("%d", &a[i]); } (1) ; for(i=1; i for(j=0, len=0; (2) ; j++) { if( (3) && len len=b[j]; } (4) ; } Printf("len:%d\n", maxL(b,n)); printf("\n"); } 【问题1】(8分) 根据说明和C代码,填充C代码中的空(1)~(4)。 【问题2】(4分) 根据说明和C代码,算法采用了 (5) 设计策略,时间复杂度为 (6) (用O符号表示)。 【问题3】(5分) 已知数组a={3,10,5,15,6,8},据说明和C代码,给出数组b的元素值。
阅读下列说明和C代码,回答问题1至问题3,将解答写在答题纸的对应栏内。
【说明】
n-皇后问题是在n行n列的棋盘上放置n个皇后,使得皇后彼此之间不受攻击,其规则是任意两个皇后不在同一行、同一列和相同的对角线上。
拟采用以下思路解决n-皇后问题:第i个皇后放在第i行。从第一个皇后开始,对每个皇后,从其对应行(第i个皇后对应第i行)的第一列开始尝试放置,若可以放置,确定该位置,考虑下一个皇后;若与之前的皇后冲突,则考虑下一列;若超出最后一列,则重新确定上一个皇后的位置。重复该过程,直到找到所有的放置方案。
【C代码】
下面是算法的C语言实现。
(1)常量和变量说明
pos:一维数组,pos[i]表示第i个皇后放置在第i行的具体位置。
count:统计放置方案数。
i,j,k:变量。
N:皇后数。
(2)C程序
#include <stdio.h>
#include <math.h>
#define N4
//*判断第k个皇后目前放置位置是否与前面的皇后冲突
in isplace(int pos[],int k)
{
int i;
for(i=1; i<k; i++)
{
if( (1) || fabs(i-k) ══fabs(pos[i] - pos[k]))
{return();}}
return 1;
}
int main()
{
int i,j,count=1;
int pos[N+1];
//初始化位置
for(i=1;
i<=N; i++)
{
pos[i]=0;}(2) ;
while(j>=1) {pos[j]= pos[j]+1;
/*尝试摆放第1个皇后
/while(pos[j]<=N&&(3)_)
{
pos[j]= pos[j]+1;}/
得到一个摆放方案
/if(pos[j]<=N&&j══ N)
{
printf("方案%d: ",count++);
for(i=1; i<=N; i++)
{
printf("%d",pos[i]);
}
printf("\n");}/
考虑下一个皇后
/if(pos[j]<=N&&(4) )
{
j=j+1;
} else{ //返回考虑上一个皇后
pos[j]=0;(5) ;
}
}return 1;}。
【问题1】(10分)
根据以上说明和C代码,填充C代码中的空(1)~(5)。
【问题2】(2分)
根据以上说明和C代码,算法采用了(6)设计策略。
【问题3】(3分)
上述C代码的输出为:(7)。