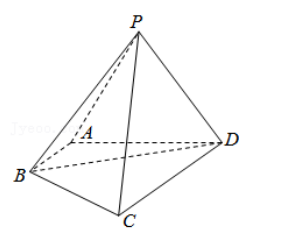
如图, 在四棱锥 P﹣ ABCD 中, AB⊥AP, AB∥CD, 且 PB=BC=BD, CD=2AB.
(Ⅰ ) 求证: 平面 PAD⊥平面 ABCD;
(Ⅱ) 若△PAD 是边长为 2 的正三角形, 且 PB 与 CD 所成角的正切值为√2, 求四棱锥 P﹣ ABCD 的体积.

如图, 在四棱锥 P﹣ ABCD 中, AB⊥AP, AB∥CD, 且 PB=BC=BD, CD=2AB.
(Ⅰ ) 求证: 平面 PAD⊥平面 ABCD;
(Ⅱ) 若△PAD 是边长为 2 的正三角形, 且 PB 与 CD 所成角的正切值为√2, 求四棱锥 P﹣ ABCD 的体积.


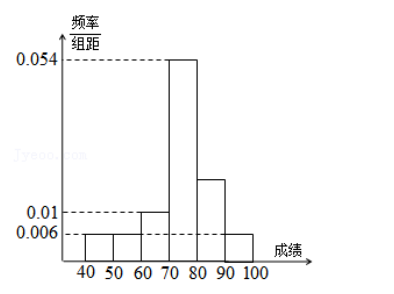
某班 50 位学生地理检测成绩的频率分布直方图如图所示, 其中成绩分组区间是: [40, 50)、 [50, 60)、 [60, 70)、 [70, 80)、 [80, 90)、 [90, 100].
(Ⅰ ) 求图中[80, 90) 的矩形高的值;
(Ⅱ ) 根据直方图求出这 50 人成绩的众数和中位数(精确到 0.1);
(Ⅲ) 从成绩在[40, 60) 的学生中随机选取 2 人, 求这 2 人成绩分别在[40, 50)、 [50,60) 的概率.

点 P 在焦点为 F 1 (﹣ c, 0)、 F 2 (c, 0) 的椭圆 C 上, PF 1 交 y 轴于点 Q, 且△PQF 2为正三角形, 若|OQ|=1, 则椭圆 C 的标准方程为


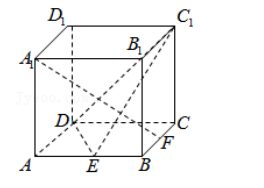
如图, 已知 E、 F 分别为正方体 ABCD﹣ A 1 B 1 C 1 D 1 的棱 AB、 BC 的中点, 平面 DEC 1 交棱 BB 1 于点 G, 则下列结论中正确的是()