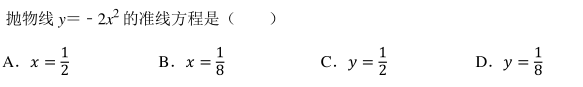
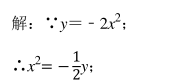

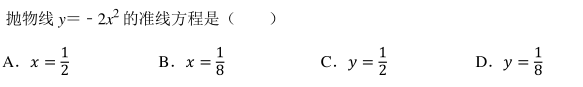
中国古代数学著作《算法统宗》 中有这样一个问题:“九百九十六斤绵, 赠分八子作盘缠,次第每人多十七, 要将第八数来言, 务要分明依次弟, 孝和休惹外人传. ” 其意思为:“996斤棉花, 分别赠送给 8 个子女作旅费, 从第一个开始, 以后每人依次多 17 斤, 使孝顺子女的美德外传, 试求各人应分得多少斤. ” 则第 3 个子女分得棉花()
若 i(x+yi) =3+4i, x, y∈R, 则复数 x+yi 的模是()
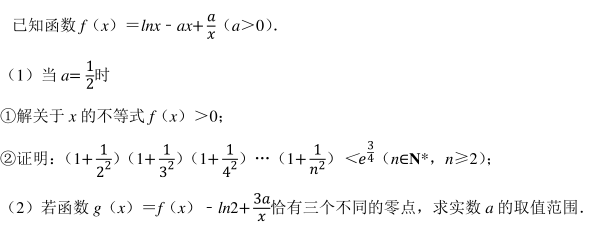
在直角坐标系 xOy 中, 以坐标原点为极点, x 轴正半轴为极轴建立极坐标系,曲线 C 的极坐标方程为 ρ=2√2cosθ.
(1) 将 C 的极坐标方程化为直角坐标方程;

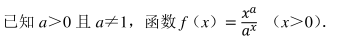
(1) 当 a=2 时, 求 f(x) 的单调区间;
(2) 若曲线 y=f(x) 与直线 y=1 有且仅有两个交点, 求 a 的取值范围
抛物线 C 的顶点为坐标原点 O, 焦点在 x 轴上, 直线 l: x=1 交 C 于 P, Q 两点, 且 OP⊥OQ. 已知点 M(2, 0), 且⊙M与 l 相切.
(1) 求 C, ⊙M的方程;
(2) 设 A 1 , A 2 , A 3 是 C 上的三个点, 直线 A 1 A 2 , A 1 A 3 均与⊙M 相切. 判断直线 A 2 A 3与⊙M的位置关系, 并说明理由.
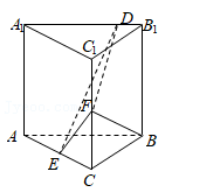
已知直三棱柱 ABC﹣ A 1 B 1 C 1 中, 侧面 AA 1 B 1 B 为正方形, AB=BC=2, E, F分别为 AC 和 CC 1 的中点, D 为棱 A 1 B 1 上的点, BF⊥A 1 B 1 .
(1) 证明: BF⊥DE;
(2) 当 B 1 D 为何值时, 面 BB 1 C 1 C 与面 DFE 所成的二面角的正弦值最小?
已知数列{a n }的各项均为正数, 记 S n 为{a n }的前 n 项和, 从下面①②③中选取两个作为条件, 证明另外一个成立
