
平面内有 2n 个点(n≥2) 等分圆周, 从 2n 个点中任取 3 个, 可构成直角三角形的概率为3/11,
连接这 2n 个点可构成正多边形, 则此正多边形的边数为()

已知全集为 U, 集合 A, B 为 U的子集, 若(∁ U A) ∩ B=∅, 则 A∩ B=()
已知函数 f(x) =|2x+4|﹣ |x﹣ 1|.
(1) 求不等式 f(x) >0 的解集
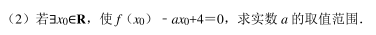


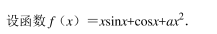



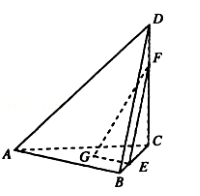
如图, 在三棱锥 D﹣ ABC 中, G 是△ABC 的重心, E, F 分别在 BC, CD 上,且BE=1/2EC,DF=1/2FC
(1) 证明: 平面 GEF∥平面 ABD;
(2) 若 CD⊥平面 ABC, AB⊥BC, AC=CD=2, BC=1, P 是线段 EF上一点, 当线段GP 长度取最小值时, 求二面角 P﹣ AD﹣ C 的余弦值.