赤道平面内的某颗卫星自西向东绕地球做圆周运动该卫星离地面的高度小于地球同步卫星的高度， 赤道上一观测者发现， 该卫星连续两次出现在观测者正上方的最小时间间隔为 t， 已知地球自转周期为 T 0 ， 地球半径为 R， 地球表面的重力加速度为 g， 由此可知该卫星绕地球运动的周期 T和离地面的高度 H为（）
赤道平面内的某颗卫星自西向东绕地球做圆周运动该卫星离地面的高度小于地球同步卫星的高度， 赤道上一观测者发现， 该卫星连续两次出现在观测者正上方的最小时间间隔为 t， 已知地球自转周期为 T 0 ， 地球半径为 R， 地球表面的重力加速度为 g， 由此可知该卫星绕地球运动的周期 T和离地面的高度 H为（）
如图所示， 质量为 2kg 的椰子从距地面高度为 20m 的树上由静止落下， 将沙地砸出小坑后静止， 与沙地接触时间约为 0.01s。 不计椰子下落时的空气阻力， 取 g＝10m/s 2 。 则（）
在核电站发生核事故后， 附近可检测出放射性元素铯 137， 铯 137的半衰期约为 30 年。 假设一条海鱼在 15 年前体内有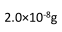
的铯 137， 若铯 137 在这期间未被代谢出体外， 则现在残留在其体内的铯 137 有（ ）
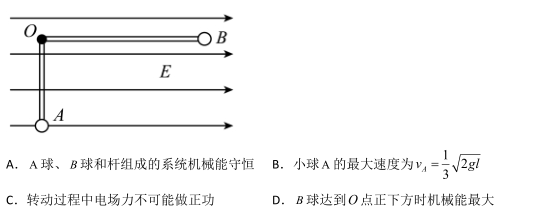
如图所示， 水平向右的匀强电场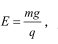
质量分别为 m、2m的小球A、B固定在直角形轻质绝缘轻杆两端， 顶点O处有固定的光滑转动轴，BO=2AO=l ， 球带电量为 +q，A球不带电，重力加速度为g，此装置从图示位置静止释放后的转动过程中，下列说法正确的是（）
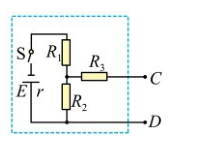
如图所示电路中， 电源电动势 E＝24 V， 恒定内阻 r＝4Ω， 定值电阻 R 1 ＝8Ω， 定值电阻 R 2 ＝12Ω， 定值电阻 R 3 ＝3Ω。 若在 C 、 D 间连接一个可调电阻 R， 调节范围为 3Ω 至 15Ω， 下列选项中正确的是（）
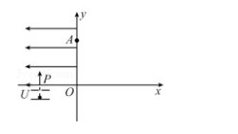
如图所示， 在平面直角坐标系 xOy 的第一象限内存在垂直于坐标平面的匀强磁场（未画出）， 第二象限存在水平向左的匀强电场。 质量为 m、 电荷量为﹣ q 的带电粒子从第三象限无初速度释放后， 经电压为 U 的电场加速后从 P（−√3L， 0） 点垂直 x 轴进入第二象限， 然后从 A（0， 2L） 点进入第一象限， 又经磁场偏转后垂直 x 轴进入第四象限。 不计粒子重力。
（1） 求第二象限内电场强度的大小；
（2） 若第一象限内的磁场方向垂直于坐标平面向里， 求磁场的磁感应强度大小；
（3） 若第一象限某矩形区域内存在匀强磁场， 磁场方向垂直于坐标平面向外， 磁感应强度大小取第（2） 问计算结果， 求矩形区域的最小面积。
如图所示， 质量 m 1 ＝3kg 的长木板与质量 m 2 ＝1kg 的1/4光滑圆弧轨道紧靠在一起静止在光滑水平面上， 圆弧轨道的下端与长木板等高， 上端与右侧的平台在同一水平面上。 质量 m 0 ＝1kg 的滑块以水平速度 v 0 ＝10m/s 从左端滑上长木板， 通过长木板后又滑上圆弧轨道， 当滑块滑离圆弧轨道最高点的瞬间， 圆弧轨道撞上右侧平台。 已知长木板长度 L＝3.8m， 滑块与长木板间的动摩擦因数 μ＝0.2， 圆弧轨道半径 R＝0.225m， 重力加速度 g＝10m/s 2 ， 求：
（1） 滑块在长木板上运动的时间及刚滑离长木板时的速度大小；
（2） 分析滑块能否落在平台上； 如果能够落在平台上， 则计算它从离开圆弧轨道到落在平台上所需时间。
2020 年 3 月 4 日环球网消息， 北京海关采样检测和排查转运地方检出核酸阳性病例 1 例， 图示为北京海关关员通过负压隔离单元对疑似病例进行隔离转运。 北京海关使用的 FU﹣ 221 生物安全型负压隔离单元， 内部尺寸为 2000mm×900mm×1800mm（长、宽、 高）， 它不工作时为密闭状态， 工作时通过顶部循环过滤的进、 排气高效净化系统保证隔离单元内为微负压环境及内部空气流通， 为疑似病人提供新鲜空气， 同时保护周围人员及周围环境不受病源体污染。 已知大气压强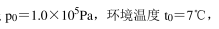
负压隔离单元停止工作且温度 t＝27℃时， 内部压强比外界低 20Pa， 空气视为理想气体，热力学温度与摄氏温度之间的关系为 T＝t+273K， 求： （计算结果均保留两位有效数字）
（1） 负压隔离单元停止工作且内部温度与外界相同时的内部气体的压强；
（2） 已知温度为 0℃、 大气压强为 1.0×l0 5 Pa 时， 空气的密度为 1.29kg/m 3 ， 计算负压隔离单元停止工作且温度 t＝27℃时内部空气的质量。
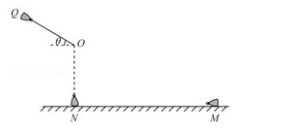
某建筑工人从高处向楼下运送细沙时， 想出了一个巧妙的办法， 如图所示， 在树杈上的 O 点系一长度为 R 的轻质细绳， 绳子另一端系铁钩（重力和大小忽略不计），在阳台上 Q 点拉直绳子并将铁钩勾住沙袋， OQ 与水平方向的夹角为 θ＝30° ， 将沙袋由静止释放， 沙袋运动到 O 点正下方 N 点时正好脱钩（脱钩过程中， 沙袋无能量损失），沿水平地面滑到 M 点停下。 已知沙袋可视为质点， 质量为 m， O、 N 两点之间的距离为R， M、 N 两点之间的距离为 2R， 重力加速度为 g， 空气阻力不计， 求：
（1） 沙袋运动到 N 点时的速度大小；
（2） 沙袋运动到 N 点脱钩前瞬间绳子的张力大小及沙袋与地面间的动摩擦因数。
某同学要测定一节干电池的电动势和内阻， 实验室备有下列器材：
