如图所示, 在直角坐标系 xOy 平面内有两个同心圆, 圆心在坐标原点O, 小圆内部(I 区) 和两圆之间的环形区域(Ⅱ 区) 存在方向均垂直 xOy 平面向里的匀强磁场(图中未画出) , I、 Ⅱ 区域磁场磁感应强度大小分别为 B、 2B。 a、 b两带正电粒子从 O 点同时分别沿 y 轴正向、 负向运动, 已知粒子 a 质量为 m、 电量为 q、 速度大小为 v, 粒子 b 质量为 2m、 电量为 2q、 速度大小为 v/2, 粒子 b恰好不穿出 1 区域, 粒子 a 不穿出大圆区域, 不计粒子重力, 不计粒子间相互作用力。
求: (1) 小圆半径 R 1 ；
(2) 大圆半径最小值
(3) a、 b 两粒子从 O 点出发到在 x 轴相遇所经过的最短时间 t(不考虑 a、 b 在其它位置相遇) 。
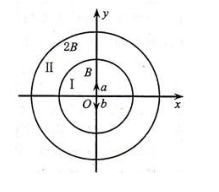
如图所示, 在直角坐标系 xOy 平面内有两个同心圆, 圆心在坐标原点O, 小圆内部(I 区) 和两圆之间的环形区域(Ⅱ 区) 存在方向均垂直 xOy 平面向里的匀强磁场(图中未画出) , I、 Ⅱ 区域磁场磁感应强度大小分别为 B、 2B。 a、 b两带正电粒子从 O 点同时分别沿 y 轴正向、 负向运动, 已知粒子 a 质量为 m、 电量为 q、 速度大小为 v, 粒子 b 质量为 2m、 电量为 2q、 速度大小为 v/2, 粒子 b恰好不穿出 1 区域, 粒子 a 不穿出大圆区域, 不计粒子重力, 不计粒子间相互作用力。
求: (1) 小圆半径 R 1 ；
(2) 大圆半径最小值
(3) a、 b 两粒子从 O 点出发到在 x 轴相遇所经过的最短时间 t(不考虑 a、 b 在其它位置相遇) 。
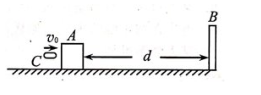
如图所示, 质量为 M 的木块 A 静置于水平面上, 距 A 右侧 d 处有固定挡板 B, 一质量为 m 的小物体 C, 以水平速度 v 0 与 A 相碰, 碰后 C、 A 粘连在一起运动, CA 整体与 B 碰撞没有能量损失, 且恰好能回到 C、 A 碰撞时的位置所有碰撞时间均不计, 重力加速度为 g。 求:
(1) C 与 A 碰撞前后, C 损失的机械能；
(2) 木块 A 与水平面间动摩擦因数μ 。
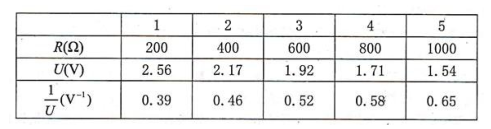
某学习小组利用图 1 所示电路测电压表内阻。 所用实验器材有: 电源E(内阻不计) , 电阻箱 R(最大阻值为 9999Ω ) , 待测电压表, 开关 S, 导线若干。
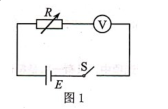
(1) 按图 1 实验电路图将图 2 实物连线。
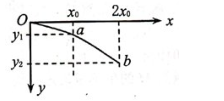
某同学在探究“平抛运动” 实验中, 在白纸上记录了竖直方向, 并作出小球平抛轨迹的部分拟合图线, 但是没有记录平抛运动的起点, 于是该同学以这段图线的起点作为坐标原点 O, 竖直向下方向为 y 轴正向, 建立直角坐标系xOy, 如图所示, 在图线上标注 a、 b 两点, 用刻度尺测得其坐标 a(x 0 , y 1 ) 、b(2x 0 , y 2 ) , 已知当地重力加速度为 g, 不计空气阻力, 则可确定:
(1) 小球由 O 运动到 b 点时间 t= ；
(2) 平抛运动的初速度大小 v 0 = ；
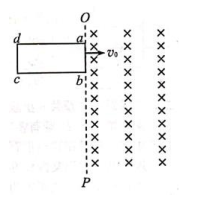
如图所示, 竖直虚线 OP 右侧有范围足够大的水平匀强磁场, 质量为 m、 电阻为 R 的矩形线框 abcd 在竖直面内, ab=cd=L, ad=bc=2L, 其 ab 边从靠近虚线 OP 处以大小为 v 0 的水平速度进入磁场, 当 ab 边进入磁场水平位移大小为 L 时, 线框的加速度大小恰好为 g, g 为重力加速度, 运动过程中线框 ad 边始终水平, 则
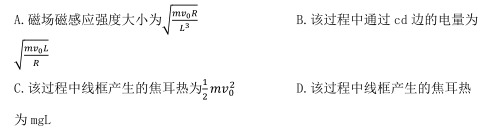
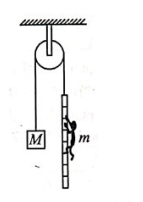
如图所示, 滑轮固定于天花板, 轻绳一端连接质量为 M 的重物, 另一端连接一梯子, 梯子上有质量为 m 的人, 重物和人均处于静止状态。 若人在梯子上对地做某种运动时, 滑轮对天花板的作用力为零, 滑轮和轻绳质量均不计, 轻绳伸长不计且轻绳始终处于伸直状态, 不计空气阻力和滑轮摩擦力, 重力加速度为 g。 下列说法正确的是
关于两个方程: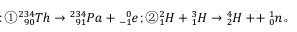
以下说法正确的是
如图, 质量为 m 的小物块初动能为 Ek0 , 从底端沿足够长的均匀粗糙斜面向上运动, 最后返回斜面底端。 已知小物块沿斜面下行时间是上行时间的 2 倍, 不计空气阻力, 下列说法正确的是
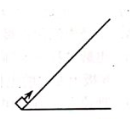
如图所示, 空间有匀强电场(图中未画出) 和水平匀强磁场, 与磁场垂直的竖直面内, 有一带电小球从 M 沿直线运动到 M, MN 与水平方向夹角为α , 下列说法可能正确的是
2019 年 2 月 , 国产科幻电影《流浪地球》 的上映引起了人们对天体运动的极大兴趣。 设想有质量为 m 的卫星绕质量为 M 的星球做匀速圆周运动, 运动半径为 R, 以卫星距该星球中心无限远处势能为零, 当卫星距该星球中心距离为 r 时,
