【说明】

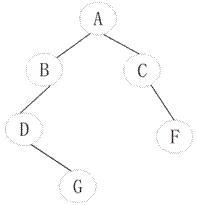
　　一棵非空二叉树中“最左下”结点定义为：若树根的左子树为空，则树根为“最左下”结点；否则，从树根的左子树根出发，沿结点的左孩子分支向下查找，直到某个结点不存在左孩子时为止，该结点即为此二叉树的“最左下”结点。例如：下图所示的以A为根的二叉树的“最左下”结点为D，以C为根的子二叉树中的“最左下”结点为C。二叉树的结点类型定义如下：

　　typedef struct BSTNode {

　　　int data ;

　　　struct BSTNode *lch ， *rch; //结点的左、右孩子指针

　} *BSTree;

函数BSTree Find_Del (BSTree root )的功能是：若root指向一棵二茶树的根结点，则找出该结点的右子树上的“最左下”结点 *p，并从树中删除以 *p为根的子树，函数返回被删除子树的根结点指针；若该树根的右子树上不存在“最左下”结点，则返回空指针。

【函数】

　　BSTree Find_Del (BSTree root)

　{ 　BSTree p， pre;

　　　If ( !root ) return NULL; /* root 指向的二叉树为空树 */

　　　　　___（1）___ ; /* 令p指向根结点的右子树 */

　　　if ( !p ) return NULL;

　　　　　___（2）___ ; /* 设置 pre 的初值 */

　　　while ( p -> lch ) { /* 查找“最左下”结点 */

　　　　　pre = p ; p = __（3）__ ;

　　}

　　　if ( __（4）__ = = root ) /* root的右子树根为“最左下”结点*/

　　　　　pre -> rch =NULL;

　　　else

　　　　　__（5）__ = NULL; /* 删除以“最左下”结点为根的子树*/

　　　return p;

　}

（）（15分，每空3分）

【说明】

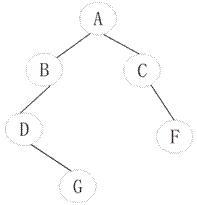
　　一棵非空二叉树中“最左下”结点定义为：若树根的左子树为空，则树根为“最左下”结点；否则，从树根的左子树根出发，沿结点的左孩子分支向下查找，直到某个结点不存在左孩子时为止，该结点即为此二叉树的“最左下”结点。例如：下图所示的以A为根的二叉树的“最左下”结点为D，以C为根的子二叉树中的“最左下”结点为C。二叉树的结点类型定义如下：

　　typedef struct BSTNode {

　　　int data ;

　　　struct BSTNode *lch ， *rch; //结点的左、右孩子指针

　} *BSTree;

函数BSTree Find_Del (BSTree root )的功能是：若root指向一棵二茶树的根结点，则找出该结点的右子树上的“最左下”结点 *p，并从树中删除以 *p为根的子树，函数返回被删除子树的根结点指针；若该树根的右子树上不存在“最左下”结点，则返回空指针。

【函数】

　　BSTree Find_Del (BSTree root)

　{ 　BSTree p， pre;

　　　If ( !root ) return NULL; /* root 指向的二叉树为空树 */

　　　　　___（1）___ ; /* 令p指向根结点的右子树 */

　　　if ( !p ) return NULL;

　　　　　___（2）___ ; /* 设置 pre 的初值 */

　　　while ( p -> lch ) { /* 查找“最左下”结点 */

　　　　　pre = p ; p = __（3）__ ;

　　}

　　　if ( __（4）__ = = root ) /* root的右子树根为“最左下”结点*/

　　　　　pre -> rch =NULL;

　　　else

　　　　　__（5）__ = NULL; /* 删除以“最左下”结点为根的子树*/

　　　return p;

　}

查看答案 纠错

答案：

本题解析：

（1） p=root->rch

（2） pre =root

（3） p->lch

（4） pre

（5） pre->lch

更新时间：2021-12-07 18:15

你可能感兴趣的试题

问答题

【说明】

　　假设一个剧场有N*N个座位，顾客买票时可以提出任意有效的座号请求。下面用二维数组a[N][N]模拟剧场中的座位，a[i][j]等于0表示第i排第j列(0≤I ， j≤N-1）的票尚未售出。

　　函数int Find ( int a[][N] ， int R ， int *row ， int *col )的功能是：在部分票已售出的情况下，找出剧场中的R*R个空座位，要求这些座位的排列形成一个正方形。若找到满足要求的一个座位排列，则函数返回1，并算出该正方形左上角的行、列号；若未找到，返回0；

　　例如，一个7×7个座位的剧场如下图(a)所示，已售出部分座位的剧场如下图(b)所示，图中阴影部分表示已售出的座位，从图(b)中找出3×3正方形空座位如图(c)中斜线区所示。

函数】

　　int Find ( int a[][N] ， int R ， int *row ， int *col )

　{ 　int i，j，k，c，t; int FOUND = 0;

　　　　for ( i=0 ; !FOUND && i　　　　　__（1）__ ;

　　　while ( j 　　　　for ( k=0; ___（2）___ && a[i][j+k] = = 0; k++)；/* 查找第i排连续的R个空座位 */

　　　if ( k >=R ){ /* 查找第i排连续的R个空座位 */

　　　　for ( c=0 ; c ＜ R ; c++ ) { /* 查找其余的R*(R-1）个座位 */

　　　　for ( t = 1 ; t ＜ R ; t++ )

　　　if (a[ __（3）__ ] [j+c] !=0 ) break;

　　if ( t 　　} /* for */

　if ( ___（4）___ ) FOUND =1;

　} /* if */

　　___（5）___ ;

　} /* while */

　} /* for i */

　if ( FOUND ) {

　　　　*row = i-1 ; *col = j-1; /* 计算正方形区域的左上角坐标*/

　　　return 1;

　　　}

　return 0;

　}

（）（15分，每空3分）

【说明】

　　假设一个剧场有N*N个座位，顾客买票时可以提出任意有效的座号请求。下面用二维数组a[N][N]模拟剧场中的座位，a[i][j]等于0表示第i排第j列(0≤I ， j≤N-1）的票尚未售出。

　　函数int Find ( int a[][N] ， int R ， int *row ， int *col )的功能是：在部分票已售出的情况下，找出剧场中的R*R个空座位，要求这些座位的排列形成一个正方形。若找到满足要求的一个座位排列，则函数返回1，并算出该正方形左上角的行、列号；若未找到，返回0；

　　例如，一个7×7个座位的剧场如下图(a)所示，已售出部分座位的剧场如下图(b)所示，图中阴影部分表示已售出的座位，从图(b)中找出3×3正方形空座位如图(c)中斜线区所示。

【函数】

　　int Find ( int a[][N] ， int R ， int *row ， int *col )

　{ 　int i，j，k，c，t; int FOUND = 0;

　　　　for ( i=0 ; !FOUND && i　　　　　__（1）__ ;

　　　while ( j 　　　　for ( k=0; ___（2）___ && a[i][j+k] = = 0; k++)；/* 查找第i排连续的R个空座位 */

　　　if ( k >=R ){ /* 查找第i排连续的R个空座位 */

　　　　for ( c=0 ; c ＜ R ; c++ ) { /* 查找其余的R*(R-1）个座位 */

　　　　for ( t = 1 ; t ＜ R ; t++ )

　　　if (a[ __（3）__ ] [j+c] !=0 ) break;

　　if ( t 　　} /* for */

　if ( ___（4）___ ) FOUND =1;

　} /* if */

　　___（5）___ ;

　} /* while */

　} /* for i */

　if ( FOUND ) {

　　　　*row = i-1 ; *col = j-1; /* 计算正方形区域的左上角坐标*/

　　　return 1;

　　　}

　return 0;

　}

查看答案

问答题

【说明】

　　一棵非空二叉树中“最左下”结点定义为：若树根的左子树为空，则树根为“最左下”结点；否则，从树根的左子树根出发，沿结点的左孩子分支向下查找，直到某个结点不存在左孩子时为止，该结点即为此二叉树的“最左下”结点。例如：下图所示的以A为根的二叉树的“最左下”结点为D，以C为根的子二叉树中的“最左下”结点为C。二叉树的结点类型定义如下：

　　typedef struct BSTNode {

　　　int data ;

　　　struct BSTNode *lch ， *rch; //结点的左、右孩子指针

　} *BSTree;

函数BSTree Find_Del (BSTree root )的功能是：若root指向一棵二茶树的根结点，则找出该结点的右子树上的“最左下”结点 *p，并从树中删除以 *p为根的子树，函数返回被删除子树的根结点指针；若该树根的右子树上不存在“最左下”结点，则返回空指针。

【函数】

　　BSTree Find_Del (BSTree root)

　{ 　BSTree p， pre;

　　　If ( !root ) return NULL; /* root 指向的二叉树为空树 */

　　　　　___（1）___ ; /* 令p指向根结点的右子树 */

　　　if ( !p ) return NULL;

　　　　　___（2）___ ; /* 设置 pre 的初值 */

　　　while ( p -> lch ) { /* 查找“最左下”结点 */

　　　　　pre = p ; p = __（3）__ ;

　　}

　　　if ( __（4）__ = = root ) /* root的右子树根为“最左下”结点*/

　　　　　pre -> rch =NULL;

　　　else

　　　　　__（5）__ = NULL; /* 删除以“最左下”结点为根的子树*/

　　　return p;

　}

（）（15分，每空3分）

【说明】

　　一棵非空二叉树中“最左下”结点定义为：若树根的左子树为空，则树根为“最左下”结点；否则，从树根的左子树根出发，沿结点的左孩子分支向下查找，直到某个结点不存在左孩子时为止，该结点即为此二叉树的“最左下”结点。例如：下图所示的以A为根的二叉树的“最左下”结点为D，以C为根的子二叉树中的“最左下”结点为C。二叉树的结点类型定义如下：

　　typedef struct BSTNode {

　　　int data ;

　　　struct BSTNode *lch ， *rch; //结点的左、右孩子指针

　} *BSTree;

函数BSTree Find_Del (BSTree root )的功能是：若root指向一棵二茶树的根结点，则找出该结点的右子树上的“最左下”结点 *p，并从树中删除以 *p为根的子树，函数返回被删除子树的根结点指针；若该树根的右子树上不存在“最左下”结点，则返回空指针。

【函数】

　　BSTree Find_Del (BSTree root)

　{ 　BSTree p， pre;

　　　If ( !root ) return NULL; /* root 指向的二叉树为空树 */

　　　　　___（1）___ ; /* 令p指向根结点的右子树 */

　　　if ( !p ) return NULL;

　　　　　___（2）___ ; /* 设置 pre 的初值 */

　　　while ( p -> lch ) { /* 查找“最左下”结点 */

　　　　　pre = p ; p = __（3）__ ;

　　}

　　　if ( __（4）__ = = root ) /* root的右子树根为“最左下”结点*/

　　　　　pre -> rch =NULL;

　　　else

　　　　　__（5）__ = NULL; /* 删除以“最左下”结点为根的子树*/

　　　return p;

　}

查看答案

问答题

阅读以下说明和C 程序，将应填入（n）处的字句写在答题纸的对应栏内。

【说明】

某旅游服务应用程序运行时，根据输入的两个城市名查找其间的距离。各城市间的距离如表4-1所示。表格中的第一行和第一列表示城市名，表中的每个元素是一个整数，代表该元素所在行和列对应的城市之间的距离（单位：km）。

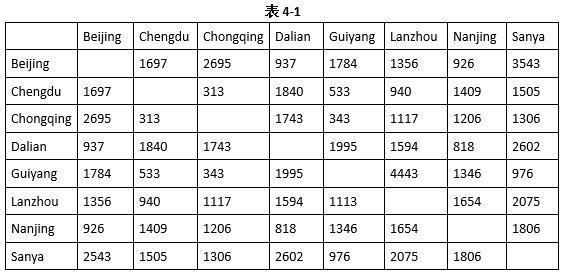
在程序中，城市名用一维全局数组cityTable存储，城市之间的距离矩阵用二维全局数组kmTable表示，并用相应的值对这两个数组进行初始化。

#define NCities 8 /* 城市个数 */

#define TRUE 1

static char * cityTable[NCities] = { /* 城市名按字典序升序排列 */

"Beijing",

...... /* 其他城市名略去 */

"Sanya",

};

static int kmTable[NCities][NCities] = {

{0, 1697, 2695, 937, 1784, 1356, 926, 2543},

{1697, 0,313, 1840,533, 940, 1409, 1505},

...... /* 剩余元素的初始值略去 */

};

程序执行时，首先按提示输入两个城市名，然后在cityTable中查找与城市名对应的下标，最后用该下标在kmTable中找到这两个城市之间的距离。

程序中定义的函数FindCityInSortedArray和GetCity说明如下：

（1）函数 FindCityInSortedArray 的功能是用二分查找法在全局数组 cityTable 中查找城市名所对应的下标值。

（2）函数GetCity的功能是读入城市名，调用函数FindCityInSortedArray来获取城市所对应的下标值。如果该城市名不存在，则提示用户重新输入。

【C 程序】

int main ( ) {

int city1，city2;

city1 = GetCity("输入第 1个城市名: ") ;

city2 = GetCity("输入第 2 个城市名: ");

printf(" %s 和%s之间的距离为：%d km.\n" ,cityTable[city1] ,

cityTable[city2] ,

kmTable[city1] [city2]);

return 0;

}

static int GetCity(char *prompt) {

char ? cityName;

int index;

cityName = (char *)malloc(20*sizeof(char));

while ( TRUE ) {

printf(" %s" ，prompt);

gets(cityName) ; /*获取输入字符串*/

index = FindCityInSortedArray(cityName);

if ( （1） ) break;

printf(" 城市名不存在，请重新输入。 \n") ;

}

free(cityName);

return （2）;

}

static int FindCityInSortedArray(char*key) {

int lh ，rh ，mid ，cmp;

lh = 0;

rh = NCities - 1;

while ( （3） ) {

mid = (lh + rh) / 2;

cmp = strcmp ( （4） ); /*比较两个城市名是否相同*/

if (cmp == 0) return （5）; /*两个城市名相同*/

if (cmp ＜ 0) { rh = mid - 1; }

else { lh = mid + 1; }

}

return (-1); /*城市名不存在时返回 -1 */

}

查看答案

问答题

阅读以下说明和C 函数，将应填入 （n） 处的字句写在答题纸的对应栏内。

【说明】

基于管理的需要，每本正式出版的图书都有一个 ISBN 号。例如，某图书的 ISBN号为“978-7-5606-2348-1”。

ISBN 号由 13 位数字组成：前三位数字代表该出版物是图书（前缀号），中间的 9个数字分为三组，分别表示组号、出版者号和书名号，最后一个数字是校验码。其中，前缀号由国际EAN提供，已经采用的前缀号为978和979；组号用以区别出版者国家、地区或者语言区，其长度可为1～5位；出版者号为各出版者的代码，其长度与出版者的计划出书量直接相关；书名号代表该出版者该出版物的特定版次；校验码采用模10加权的算法计算得出。

校验码的计算方法如下：

第一步：前 12 位数字中的奇数位数字用 1 相乘，偶数位数字用 3 相乘（位编号从左到右依次为13到2）；

第二步：将各乘积相加，求出总和S；

第三步：将总和S 除以10，得出余数R；

第四步：将10减去余数R后即为校验码V。若相减后的数值为10，则校验码为0。

例如，对于ISBN 号“978-7-5606-2348-1”，其校验码为1，计算过程为：

S=9×1+7×3+8×1+7×3+5×1+6×3+0×1+6×3+2×1+3×3+4×1+8×3=139

R = 139 mod 10 = 9

V = 10 – 9 = 1

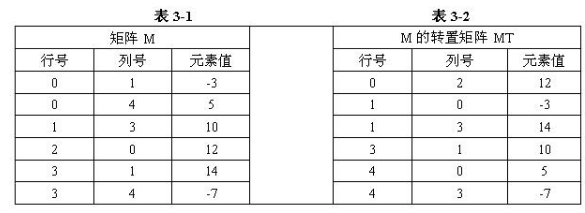
函数check(char code[])用来检查保存在code中的一个ISBN号的校验码是否正确，若正确则返回 true，否则返回 false。例如，ISBN 号“978-7-5606-2348-1”在 code 中的存储布局如表3-1所示（书号的各组成部分之间用“-”分隔）：

在函数check(char code[])中，先将13位ISBN号放在整型数组元素tarr[0]～tarr[12]中（如表3-2 所示，对应 ISBN 号的位13～位 1），由 tarr[0]～tarr[11]计算出校验码放入变量V，再进行判断。

【C 函数】

bool check(char code[ ])

{

int i,k = 0;

int S = 0 ，temp = 0;

int V ;

int tarr[13]={0};

if (strlen(code) ＜ 17) return false;

for( i=0; i＜17 ; i++ ) /*将 13位 ISBN 号存入 tarr */

if ( code [i] != '- ' )

tarr[ （1） ]= code[i] - ' 0 ';

for (i=0;（2）;i++){

if( i%2 )

S += （3） ;

else

S += （4） ;

}

V = ( （5） == 0 )? 0 ： 10 - S %10;

if ( tarr[12] == V)

return true ;

return false;

}

查看答案

问答题

阅读以下说明和C语言函数，将应填入 （n） 处的字旬写在答题纸的对应栏内。

【说明】

　　某工厂A负责为某大型企业B加工零件，A每天必须为B提供一定数量的零件。由于某种客观原因，A每天生产的零件的单价都不相同。若A某天生产的零件数多于B需要的数目，则多余的零件可以放到第二天及以后再使用，但需要收取每个零件的保管费（产品单价之外附加的费用），每个零件在不同日期收取的保管费也不相同。

　　例如，在5天的生产中，B要求的零件需求量及A核算出的零件单价和保管费用如表l所示：表1

A可以制订多种生产计划，但费用可能不同。例如，表2所示为生产计划及其费用。

表2

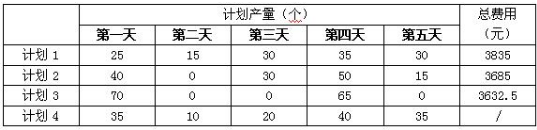
注：

　　（1）计划1的总费用：25*20+15*30+30*32+35*25+30*35=3835（元）

　　（2）计划2的总费用：40*20+15*4.5+30*32+50*25+15*5.5+15*35=3685（元）

　　（3）计划3的总费用：70*20+45*4.5+30*8+65*25+30*5.5=3632.5（元）

　　（4）计划4不可行，虽然第一天和第二天生产的零件总数比需求量多5个，但加上第三天生产的20个零件（共25个），仍不能满足B第三天的需求量（30个）。

函数find_a_plan（FILE *in）的功能是：从文件中读入若干个生产计划，从可行的计划中选出费用最小者，记录该生产计划并返回该最小费用。

　　全局结构体数组data［］用于保存表1所示的数据（data［0］不用），说明如下：

　　data［i］．Qty_req: int型，表示第i天的零件需求量。

　　data［i］．Price: double型，表示第i天生产的零件单价（元）。

　　data［i］．Keeping_fee: double型，表示第i天保管单个零件的费用（元）。

【C语言函数】

　　int B_s［DAYS+1］;/*记录成本最小的生产计划，B_s[0]不用，DAYS定义为天数*/

　　　　double find_a_plan（FILE *inf）

　　　　｛int P_num[DAYS+l]，acc_req[DAYS+1];

　　　　int i，tag = 0，acc_qty = 0;

　　double mincost = 1.0e20，cost_Produce，cost_Keep;

　　for（i=l;i＜=DAYS;i++）{/*到第i天时的累计零件需求量存入acc_req[i]*/ acc_qty += data[i].Qty_req;

　　　　acc_req[i] = acc_qty;

　　}

　　while(!feof(inf)){

　　　　for（i=1;i＜=DAYS;i++）/*未读入一个生产计划，第i天的产量存入P_num[i]*/

　　　　if(!feof(inf))

　　fscanf(inf，"%d″，＆P_num[i]);

　　tag = 0; cost_Produce = 0;cost_Keep = 0;

　　　　for(i = l， （1） ;i＜=DAYS;i++){/*考察当前的生产计划*/

　　　　acc_qty +=P_num[i];/* acc_qty计录到第i天时的累计零件生产量*/

　　if（acc_qty＜acc_req[i]）｛/*当前生产计划不能满足需求*/

　　　　tag = 1; break;

　　} /*if*/

　　cost_Produce += （2） ;/*计算当前生成计划的总零件价格*/

　　/*计算当前生成计划下的零件保管费*/

　　cost_Keep += （ （3） ） * data[i].Keeping_fee;

　　｝/*for*/

　　if（ （4） ）/*若当前生产计划不可行，则继续读取下一计划*/

　　continue;

　　if（ （5） ）/*记录成本更小的生产计划*/

　　mincost = cost_Produce + cost_Keep;

　　for（i = 1; i ＜= DAYS; i++）

　　B_s[i] = P_num[i];

　　}/*if*/

　　}/*while*/

　　return mlncost;

}

查看答案

问答题

阅读以下说明和C语言函数，将应填入 （n） 处的宇句写在答题纸的对应栏内。

【说明】

　　函数bool Del_elem（STACK *s，char para_ch）的功能是：删除栈*s中与para_ch之值相等且最接近栈项的元素（字符），若栈中不存在该元素，则函数返回FALSE，否则返回TRUE。其中，STACK是栈的类型名。

　　函数Del_elem实现上述功能的方法是：利用栈的基本操作，先将栈*s中所有比para_ch之值更接近栈顶的元素暂时存放在临时工作栈s_bak中，使得与para_ch之值相等的元素成为栈顶元素，此时执行出栈操作，即从栈中删除与para_ch之值相等的元素，最后再将s_bak中的元素依次存回栈*S。

　　在函数Del_elem中必须使用栈的基本操作进行栈上的运算，实现栈的基本操作的函数原型说明如下：

　　void InitStack（STACK *S）：初始化栈。

　　void Push（STACK *S，char e）：将一个字符压栈，栈中元素数目增1。

　　void Pop（STACK *S）：栈顶元素出栈，栈中元素数目减1。

　　char Top（STACK S）：返回非空栈的栈顶元素值，栈中元素数目不变。

　　bool IsEmpty（STACK s）：若S是空栈，则返回TRUE;否则返回FALSE。

　　bool类型定义如下：

　　typedef enum {FALSE = 0，TRUE = 1} bool;

【C语言函数】

　　bool Del_elem（STACK *s，char para_ch）

　　{

　　　　STACK s_bak; /*定义临时工作栈s_bak*/

　　　　char ch;

　　　　bool tag = FALSE;

　　　　（1） ; /*中初始化临时工作栈s_bak*/

　　/*中将栈*s中所有比para_ch更接近栈顶的元素暂时存放在临时工作栈s_bak中*/

　　　　while（!IsEmpty（*S）） {

　　　　ch = （2） ; /*取栈顶元素*/

　　　　Pop（s）;

　　　　if （ch == para_ch） {

　　　　tag = TRUE;

　　　　break;

　　　　}

　　　　（3） ;

　　}

　　/*将暂存于临时工作栈s_bak中的元素存回栈*S */

　　　　while （ （4） ） {

　　　　ch = Top（s_bak）;

　　　　（5） ;

　　　　Push（s， ch）;

　　}

　　　　return tag;

　　}

查看答案

问答题

阅读以下应用说明以及用Visual Basic编写的程序代码，将应填入(n)处的字句写在答题纸的对应栏内。

【应用4.1】

设应用程序的运行窗口内有一个文字标签（Label）以及一个框架，其中有三个复选框(chkl，chk2，chk3 )，各个复选框单击事件过程的程序代码如下：

Private Sub chkl Click（）

Label.fontBold = chkl.Value

End Sub

Private Sub chk2 Click（）

Label.fontItalic = chk2.Value

End Sub

Private Sub chk3 Click（）

Label.fontUnderLine = chk3.Value

End Sub

三个复选框chkl、chk2、chk3的功能分别是：（l ）

【应用4.2】

设应用程序的运行窗口内有两个文本框Txt 1和Txt2，其初始内容为空。在Txt 1文本框中输入一个数值，当光标离开此文本框（例如进入文本框Txt2 )时，执行的程序代码如下：

Private Sub Txtl_LostFocus（）

dim x as double

x = Val(Txtl.Text）

If x＜0 Or x＞100 Then

Txtl.Text = “ ”

MsgBox$（“请重新输入!”）

Txtl.SetFocus

Else

Txt2.Text = Txtl.Text

End If

End Sub

该程序代码的功能是：若在文本框Txt1中输入的数值小于0或大于100，当光标离开此文本框时，(2) ；否则，将其值复制到文本框Txt2中。

【应用4.3】

在下面的应用中，当窗口内发生Click事件时，窗口内将显示如图4-1所示的杨辉三角形（每一行都是三项式展开的系数）。请完善程序代码。

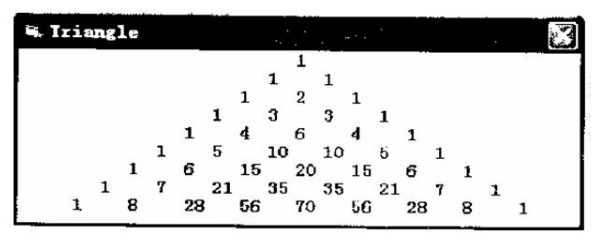
Private Sub Form Click（）

Dim i ， j ， c As Integer ， StrTemp As String

Dim a(9) As Integer

a(0) = 0 : a(1) = 1 : StrTemp = Str(a(1)) ＋ Space(3)

CurrentX = （ScaleWidth一TextWidth(StrTemp)）/2

Print StrTemp

For j = 2 To 9

a（j）= 1

For c = j-1 To 2 Step - 1

a（c） = （3）

Next

(4) = “”

For c = 1 To j

StrTemp = StrTemp & Str（(5)）& Space (5 - Len (Str (a (c)）））

Next

CurrentX =（ScaleWidth一TextWidth(StrTemp)）/ 2

Print StrTemp

Next

End Sub

（） 〔共15分）

阅读以下应用说明以及用Visual Basic编写的程序代码，将应填入(n)处的字句写在答题纸的对应栏内。

【应用4.1】

设应用程序的运行窗口内有一个文字标签（Label）以及一个框架，其中有三个复选框(chkl，chk2，chk3 )，各个复选框单击事件过程的程序代码如下：

Private Sub chkl Click（）

Label.fontBold = chkl.Value

End Sub

Private Sub chk2 Click（）

Label.fontItalic = chk2.Value

End Sub

Private Sub chk3 Click（）

Label.fontUnderLine = chk3.Value

End Sub

三个复选框chkl、chk2、chk3的功能分别是：（l ）

【应用4.2】

设应用程序的运行窗口内有两个文本框Txt 1和Txt2，其初始内容为空。在Txt 1文本框中输入一个数值，当光标离开此文本框（例如进入文本框Txt2 )时，执行的程序代码如下：

Private Sub Txtl_LostFocus（）

dim x as double

x = Val(Txtl.Text）

If x＜0 Or x＞100 Then

Txtl.Text = “ ”

MsgBox$（“请重新输入!”）

Txtl.SetFocus

Else

Txt2.Text = Txtl.Text

End If

End Sub

该程序代码的功能是：若在文本框Txt1中输入的数值小于0或大于100，当光标离开此文本框时，(2) ；否则，将其值复制到文本框Txt2中。

【应用4.3】

在下面的应用中，当窗口内发生Click事件时，窗口内将显示如图4-1所示的杨辉三角形（每一行都是三项式展开的系数）。请完善程序代码。

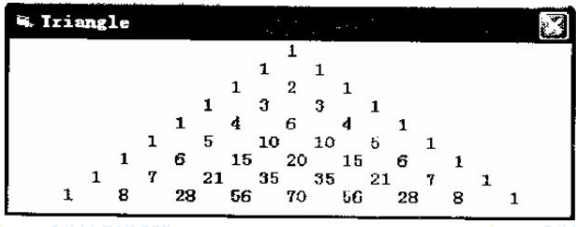
Private Sub Form Click（）

Dim i ， j ， c As Integer ， StrTemp As String

Dim a(9) As Integer

a(0) = 0 : a(1) = 1 : StrTemp = Str(a(1)) ＋ Space(3)

CurrentX = （ScaleWidth一TextWidth(StrTemp)）/2

Print StrTemp

For j = 2 To 9

a（j）= 1

For c = j-1 To 2 Step - 1

a（c） = （3）

Next

(4) = “”

For c = 1 To j

StrTemp = StrTemp & Str（(5)）& Space (5 - Len (Str (a (c)）））

Next

CurrentX =（ScaleWidth一TextWidth(StrTemp)）/ 2

Print StrTemp

Next

End Sub

查看答案

问答题

阅读以下说明和C函数，将应填入(n)处的字句写在答题纸的对应栏内。

【说明】

若一个矩阵中的非零元素数目很少且分布没有规律，则称之为稀疏矩阵对丁tm行n列的稀疏矩阵M，进行转置运算后得到n行m列的矩阵MT，如图3-1所示

图3-1稀疏矩阵M及其转置矩阵MT

为了压缩稀疏矩阵的存储空间，用三元组（即元素所在的行号、列号和元索宜、表示稀疏矩阵中的一个非零元素，再用一维数组逐行存储稀疏矩阵中的所有非零三素也称为三元组顺序表）。例如，图3-1所示的矩阵M相应的三元组顺序表如表3-1所示．其转置矩阵MT的三元组顺序表如表3-2所示。

函数TransposeMatrix(Matrix M)的功能是对用三元组顺序表表示的稀疏矩阵M进行转置运算。

对M实施转置运算时，为了将M中的每个非零元素直接存入其转置矩阵MT三元组顺序表的相应位置，需先计算M中每一列非零元素的数目（即MT中每一行非零几素的数目），并记录在向量num中；然后根据以下关系，计算出矩阵M中每列的第一个非零元素在转置矩阵MT三元组顺序表中的位置：

cpot[0] = 0

cpot[j] = cpot[ j-1]＋num[j-1]〕 /* j为列号 */

类型ElemType， Triple和Matrix定义如下：

typedef int ElemType；

typedef struct｛ /* 三元组类型 */

int r，c； /* 矩阵元素的行号、列号 */

ElemType e； /* 矩阵元素的值 */

｝Triple；

typedef struct｛ /* 矩阵的元组三元组顺序表存储结构 */

int rows，cols，elements； /* 矩阵的行数、列数和非零元素数目 */

Triple data［MAXSIZE］：

｝Matrix;

【C函数】

int TransposeMatrix(Matrix M)

｛

int j ， q ， t;

int *num， *cpot;

Matrix MT; /* MT是M的转置矩阵 */

num =（int*）malloc(M.cols*sizeof（int））;

cpot =（int*）malloc (M.cols*sizeof（int））;

if（!num || !cpot)

return ERROR;

MT. rows = (1) ; /*设置转置矩阵MT行数、列数和非零元数目*/

MT. cols =（2）;

MT.elements = M.elements;

if (M. elements > 0)｛

for (q = 0 ; q ＜ M. cols ; q++)

num[q] = 0;

for (t = 0 ; t ＜ M. elements ; ++t ) /* 计算矩阵M中每一列非零元素数目 */

num [M.data [t].c]++：

/* 计算矩阵M中每列第一个非零元素在其转置矩阵三元组顺序表中的位置 */(3) ;

for（j = 1 ; j＜M. cols ; j++）

cpot[j] = (4)：

/* 以下代码完成转置矩阵MT三元组顺序表元素的设置 */

for（t = 0 ; t＜M.elements ; t++)｛

j = (5) /* 取矩阵M的一个非零元素的列号存入j */

/*q为该非零元素在转置矩阵MT三元组顺序表中的位置（下标）*/

q = cpot[j];

MT. data[q].r = M. data[t].c;

MT. data[q].c = M. data[t].r;

MT. data[q].e = M. data[t].e;

++cpot[j]; /* 计算M中第j列的下一个非零元素的目的位置 */

｝/* for */

｝/* if */

free(num); free(cpot）;

/* 此处输出矩阵元素，代码省略 */

return OK;

｝/*TransposeMatrix*/

查看答案

问答题

阅读以下说明和C语言函数，将应填入 （n） 处的字句写在答题纸的对应栏内。

【说明】

　　函数 sort(NODE *head)的功能是：用冒泡排序法对单链表中的元素进行非递减排序。对于两个相邻结点中的元素，若较小的元素在前面，则交换这两个结点中的元素值。其中，head指向链表的头结点。排序时，为了避免每趟都扫描到链表的尾结点，设置一个指针endptr，使其指向下趟扫描需要到达的最后一个结点。例如，对于图4-1 (a)的链表进行一趟冒泡排序后，得到图4-1 (b)所示的链表。

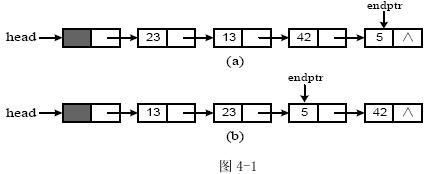
链表的结点类型定义如下：

　　　typedef struct Node {

　　　 int data;

　　　struct Node *next;

　　}NODE;

【C语言函数】

查看答案

问答题

阅读以下说明和C语言函数，将应填入 （n） 处的字句写在答题纸的对应栏内。

【说明】

　　函数 count_ months(DATE start， DATE end)的功能是：计算两个给定日期之间所包含的完整月份数。

　　该函数先算出起止日期中所含的完整年数，再计算余下的完整月份数。

规定两个相邻年份的同月同日之间的间隔为 1 年。例如，2007.5.30～2008.5.30的间隔为 1 年。若相邻两年中前一年是闰年，并且日期是 2 月 29 日，则到下一年的 2月28日为1年，即2008.2.29～2009.2.28的间隔为1年。

　　规定两个相邻月份的相同日之间的间隔为1个月，但需要特别考虑月末的特殊情况。例如，2007.1.29～2007.2.28 的间隔为 1 个月，同理，2007.1.30 30～2007.2.28、2007.1.31～2007.2.28的间隔都是1个月。

　　计算起止日期间隔不足一年的完整月份数时，分两种情况：

　　1）起止日期不跨年度。先用终止日期的月号减去起始日期的月号得到月份数，然后再根据情况进行修正。例如，起止日期为2008.3.31～2008.9.20，通过月号算出月份数为 6。修正时，通过调用函数 makevalid 将 2008.9.31 改为 2008.9.30，与终止日期2008.9.20比较后，将月份数修正为5。

　　2）起止日期跨年度。计算方法如下例所示：对于起止日期2008.7.25～2009.3.31，先计算 2008.7.25～2008.12.25的月份数为 5，再算出 2008.12.25～2009.3.25 的月份数为3，因此2008.7.25～2009.3.31之间的完整月份数为8。

　　日期数据类型定义如下：

　　　typedef struct {

　　 int year; int month; int day; /*日期的年号（4位）、月和日号*/

　　　}DATE;

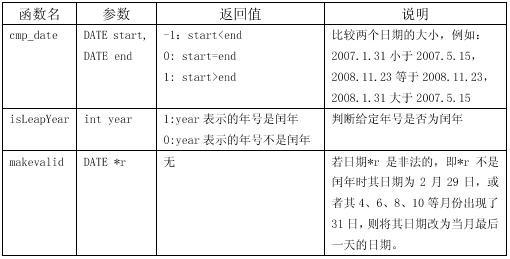
　　程序中使用的函数cmp_date()、isLeapYear()和makevalid()说明如下：

【C语言函数】

查看答案