2019年教师招聘考试《中学数学》真题精选1

试卷预览

1 单选题 1分

以下是某学生证明勾股定理“在Rt△ABC中，∠C=90°，求证a2+b2=c2”的过程：因为a=csinA，b=ccosA，所以a2+b2=c2sin2A+c2cos2A=c2(sin2A+cos2A)=c2。

以上证明所犯的错误主要是( )。

查看答案 开始考试

正确答案：C

本题解析：

该学生在论证中用到sin2A+cos2A=1，而这个公式成立依赖于a2+b2=c2，因此该学生的论证犯了循环论证的错误。

2 单选题 1分

二次方程、二次不等式、二次函数在教材中是分别研究的，为了将以上概念统一起来并从更高的角度加以认识．我们主要通过( )。

查看答案 开始考试

正确答案：B

本题解析：

二次方程可以用二次函数与x轴的交点来研究，二次不等式可以用二次函数函数值的正负来研究，所以这三个概念可以用函数思想统一起来。

3 单选题 1分

在某教师设计的“一次函数的图象和性质”的教学目标中，“在一次函数图象及性质的探究过程中．养成联系实际、善于观察、勇于探索和勤于思考的习惯”属于以下四个方面中的( )。

查看答案 开始考试

正确答案：D

本题解析：

《义务教育数学课程标准(2011年版)》中，课程目标的总目标中关于“隋感态度”方面的阐述是：积极参与数学活动，对数学有好奇心和求知欲；数学学习过程中，体验获得成功的乐趣，锻炼克服困难的意志，建立自信心；体会数学的特点。了解数学的价值：养成认真勤奋、独立思考、合作交流、反思质疑等学习习惯，形成实事求是的科学态度。

4 单选题 1分

已知函数f(x)在区间(0，1)内可导，则以下结论正确的是( )。

查看答案 开始考试

正确答案：C

本题解析：

5 单选题 1分

查看答案 开始考试

正确答案：D

本题解析：

6 单选题 1分

在yOz平面上的直线z=y绕z轴旋转一周之后得到的曲线方程为( )。

查看答案 开始考试

正确答案：A

本题解析：

直线绕z轴旋转所得为对顶圆锥，中心在原点。绕z轴旋转yOz平面上的直线z=y，将直

7 单选题 1分

命题“若x≤-2，则x2≥4”的逆否命题是( )。

查看答案 开始考试

正确答案：B

本题解析：

原命题为“若P，则q”，则逆否命题为“若非q，则非P”。即为“若x2<4，则x>-2”。

8 单选题 1分

如图，点P为⊙O上一动点，PA，PB为⊙O的两条弦，BE，AF分别垂直于PA，PB，垂足分别为E，F，若∠P=60°，⊙O的半径为4，则EF的长( )。

查看答案 开始考试

正确答案：C

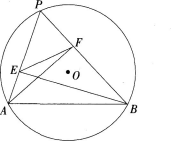
本题解析：

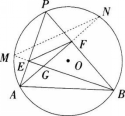
BE，AF的交点记为G，G即是△ABC垂心，则G点关于AP，BP两条边的对称点M，N都在△ABC外接圆⊙O上。(三角形的垂心关于三边的对称点都在三角形的外接圆上。)则EF是△GMN平行于 MN边的中位线，则EF∥MN,所以∠FEB=∠M=∠FAB。 又因为G为垂心，所以∠PEF+∠FEB=∠FAB+∠PBA=90°，所以∠PEF=∠PBA。所以△PEF∽△PBA，于是

9 单选题 1分

某天早上小明上学，先步行一段路，因为时间紧，他又改乘出租车，结果到校还是迟到了5分钟，其行程情况如图，若出发时直接乘出租车(车速不变)，则他( )。

查看答案 开始考试

正确答案：D

本题解析：

由图象可知步行的5百米所用时间为8分钟，出租车走35-5=30(百米)所用的时间为14—8=6(分钟)，出租车的速度为30+6=5(百米／分钟)。如果他出发时直接乘出租车，前5百米所用的时间为5÷5=1(分钟)，比原来要节省8-1=7(分钟)。又因为迟到了5分钟，所以如果他出门时直接乘出租车则可提前2分钟到校。

10 单选题 1分

我国古代《易经》一书中记载，远古时期人们通过在绳子上打结来记录数量，即“结绳计数”。如图，一位母亲在从右到左依次排列的绳子上打结，满七进一，用来记录孩子自出生后的天数，由图可知，孩子自出生后的天数是( )。

查看答案 开始考试

正确答案：C

本题解析：

从右侧开始第一列五个结表示5x1=5天，第二列两个结表示2x7=14天，第三列三个结表示3x(7×7)=147天，第四列一个结表示1x[7x(7x7)]=343，故孩子出生后的总天数为5+14+147+343=509天。