推荐等级:
发布时间: 2021-08-25 07:59
扫码用手机做题
平面四连杆机构ABCD如图所示,如杆AB以等角速度ω=1rad/s绕A轴顺时针向转动,则CD杆角速度ωCD的大小和方向为( )。
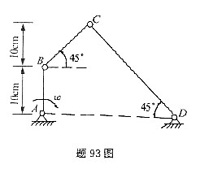
本题解析:
CB平面运动,速度投影定理,
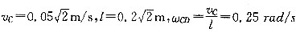
一简支梁长为5m,剪力图如图所示,错误的答案是( )。
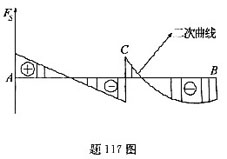
本题解析:
因为在C截面上FS有向上的跃变,因而有向上的集中荷载。AC段是有向下倾的直线,因而有指向下的均布荷载。CB段为向下凸的二次曲线,因而有指向下的三角形分布荷载。因为集中力偶对剪力没有显式影响,所以不能确定该简支梁是否有集中力偶
图示结构,AC为铝杆,AAC=200mm2,lAC=2.5m,EAC=70GPa;BC杆为钢杆,ABC=250mm2,lBC=4m,EBC=200GPa。F=50kN,则( )。
本题解析:
由节点c的平衡关系得杆Ac和BC的内力,再根据胡克定律
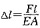
即得
一平面简谐波表达式为y=0.5sinπ(t-2x)(SI),则该波的频率v(Hz),波速u(m/s)及波线上各点振动的振幅A(m)依次为( )。
本题解析:
波的表达式为,比较两式得到
下列关于温度的意义的描述,正确的是( )。
①气体的温度是分子平均平动动能的量度;
②气体的温度是大量气体分子热运动的集体表现,具有统计意义;
③温度的高低反映物质内部分子运动剧烈程度的不同;
④从微观上看,气体的温度表示每个气体分子的冷热程度。
本题解析:
由公式可知,气体的温度是气体分子平均平动动能的量度,对个别分子来说它有温度是没有意义的
曲面z=x2+y2-1在点(1,-1,1)处的切平面方程是( )。
本题解析:
设F(x,y,z)=x2+y2-z-1,则点(1,-1,1)处的切平面法向量为n=(Fx,Fy,Fz)(1,-1,1)={2x,2y,-1)(1,-1,1)={2,-2,-1),利用平面的点法式方程公式即可得解
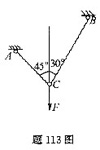
图示机构中各杆的自重不计,BC杆水平,α=30°,在C点悬挂重物的重力大小W=1500kN,在B点作用一力P,其大小等于500kN,设它与铅直线的夹角为θ。则当机构平衡时,θ角的大小为( )。
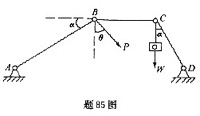
本题解析:
分别研究B点及C点,且分别列垂直于AB及DC轴的投影方程
某项目有甲、乙、丙、丁四个投资方案,寿命期限都是8年,基准折现率10%,(P/A,10%,8)=5.335,各年的净现金流量如下表所示:

采用净现值法应选用方案( )。
本题解析:
甲、乙年净收益相等.但乙方案投资较小,所以淘汰甲方案;丙、丁方案投资额相等,但丙方案年收益率较大,淘汰丁方案;比较乙、丙方案的净现值
试卷分类:电气工程师公共基础
练习次数:16次
试卷分类:电气工程师公共基础
练习次数:17次
试卷分类:电气工程师公共基础
练习次数:18次
试卷分类:电气工程师发输变电专业
练习次数:18次
试卷分类:电气工程师供配电专业
练习次数:17次
试卷分类:电气工程师基础专业知识
练习次数:17次
试卷分类:电气工程师公共基础
练习次数:17次
试卷分类:电气工程师公共基础
练习次数:18次
试卷分类:电气工程师公共基础
练习次数:18次
试卷分类:电气工程师公共基础
练习次数:24次