当前位置:首页 → 职业资格 → 教师资格 → 中学数学学科知识与教学能力->教学设计。阅读下述材料回答问题。在学习了等比数列前n项和公式
教学设计。阅读下述材料回答问题。
在学习了等比数列前n项和公式后,数学老师李老师给大家留了一道思考题:“你能把无限循环小数化成分数吗?你用的什么方法,用具体的例子说明。”李老师将这个问题留作作业,让大家写一个小的总结。有的同学表示,第一次做这样的作业,没有具体的题目,不知道如何下手。还有的同学觉得老师留的问题不够具体,不知道写到什么程度。
问题:
(1)说说你对李老师留这样的作业的看法。
(2)李老师在批阅了大家的作业后,要针对学生的作答情况在课堂上做一个总结.请以“把无限循环小数化成分数”为教学
(1)李老师打破了传统教学的思路,留的作业有一定的开放性、探究性,并且这个问题是在学习了等比数列求和公式后紧接着给出的,学生“跳一跳能够到”。解决这个问题学生可以找到所学知识(等比数列的知识)内在的联系,培养学生运用所学知识解决问题能力,培养学生发散思维的能力以及对所学的知识做到活学活用.学以致用的能力。
(2)教学片段
师:大家的作业我看了,大部分同学做得很好,下面我们一起来看一下这个问题。把无限循环小数化成分数,我没有给出具体哪个无限不循环小数,大家看到题首先要思考,什么样的小数是无限循环小数。它是怎么化成分数的。那么什么样的小数是无限循环小数呢?
生:小数点后有重复出现的数字。
师:不够严谨,应该是从小数点后某一位开始不断地重复出现前一个或一节数码的十进制无限小数。比如:
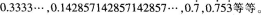
师:很多同学解决这个问题的时候想到了我们刚刚学过的等比数列前n项和公式,能利用这个知识来解决问题。要表扬大家,很棒。下面我请一位同学说一下用这种方法的思路。小贾,你来说。

师:很好,思路很清晰。把隐藏在循环小数里的等比数列求和问题挖掘出来,有一部分同学是这么做的。整个过程中运用了化归转化思想,极限思想。
师:我看到,还有一些同学有其他解法。小马,你来说说你的做法。

师:看来你对这种做法已经很熟悉了。大家发现没有,这个方法的巧妙之处在于把重复的小数分别消去了!
怎么消去的呢?
生:把原来的数扩大了。
师:扩大了多少倍。
生:……

(大部分学生都明白其中的道理了)
师:很好,大家都明白了吧。我现在想问大家,把原来的数扩大多少倍后再和原来的式子作差,这种方法我们接触过吗?
(预设)个别学生:刚刚就见过。在推导等比数列前n项和的时候就是这么推导的。前两天刚讲过,叫错位相减法。
师:很好!看来有的同学发现了,这就是在推导等比数列前n项和时用到的错位相减法。
师:小贾同学的做法是把循环小数转化成等比数列求和问题,再利用等比数列前n项和公式直接计算。
小马同学的做法是巧妙的利用循环小数本身的特点,用错位相减法解决了问题。两种办法都很好,大家要把这两种方法都学会。这个问题我们课堂上就讨论这两种方法,同学课下再相互交流一下还有没有其他的做法。
有“泥土诗人”之称的诗人是()。
将下列各项按所表示年龄大小顺序排列,正确的顺序应是( )。
①不惑②垂髫③花甲④加冠⑤而立⑥古稀⑦半百
钱穆在评论中国古代某制度时说,它“可以培植全国人民对政治之兴味……可以团结全国各地域于一个中央之统治”,这一制度是()。
明朝初年强化君主专制的措施是()。
1931年,一位给人们带来光明的科学家重病的消息牵动着世界人民的心,几十名记者为他守夜。每隔一个小时就对外发布一次消息:“灯”还亮着。这位科学家是( )。
在我国历史上,传统音乐与外族音乐、北方与南方音乐进行广泛交流的时期是()。
下列哪部歌剧是瓦格纳的作品()
乐器“缶”的制作材料属于( )。
隋唐至宋,在宫廷宴饮时娱乐欣赏的音乐称为()。
双簧管属于()。