已知直三棱柱 ABC﹣ A 1 B 1 C 1 中, 侧面 AA 1 B 1 B 为正方形, AB=BC=2, E, F分别为 AC 和 CC 1 的中点, D 为棱 A 1 B 1 上的点, BF⊥A 1 B 1 .
(1) 证明: BF⊥DE;
(2) 当 B 1 D 为何值时, 面 BB 1 C 1 C 与面 DFE 所成的二面角的正弦值最小?
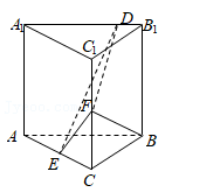


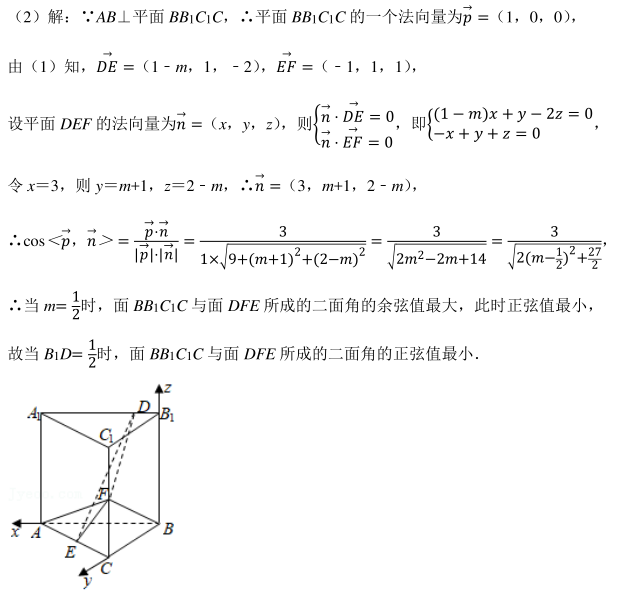
已知直三棱柱 ABC﹣ A 1 B 1 C 1 中, 侧面 AA 1 B 1 B 为正方形, AB=BC=2, E, F分别为 AC 和 CC 1 的中点, D 为棱 A 1 B 1 上的点, BF⊥A 1 B 1 .
(1) 证明: BF⊥DE;
(2) 当 B 1 D 为何值时, 面 BB 1 C 1 C 与面 DFE 所成的二面角的正弦值最小?

已知数列{a n }的各项均为正数, 记 S n 为{a n }的前 n 项和, 从下面①②③中选取两个作为条件, 证明另外一个成立

近几年, 随着大众鲜花消费习惯的转变, 中国进入一个鲜花消费的增长期. 根据以往统计, 某地一鲜花店销售某种 B 级玫瑰花, 在连续统计的 320 天的玫瑰花售卖中,每天的玫瑰花的销售量(单位: 支) 与特殊节日的天数如表:
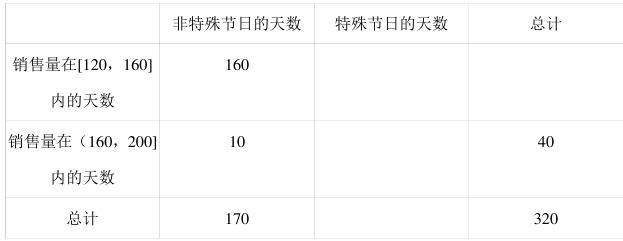
(1) 填写上表, 判断是否有 99%的把握认为“每天的玫瑰花的销售量与特殊节日有关”?
(2) 若按分层抽样的方式, 从上述表格的特殊节日中抽取 5 天作为一个样本, 再从这个样本中抽取 2 天加以分析研究, 求这两天玫瑰花的销售量在[120, 160]内的概率.



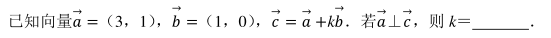

已知 A, B, C 是半径为 1 的球 O 的球面上的三个点, 且 AC⊥BC, AC=BC=1, 则三棱锥 O﹣ ABC 的体积为()

将 4 个 1 和 2 个 0 随机排成一行, 则 2 个 0 不相邻的概率为()