


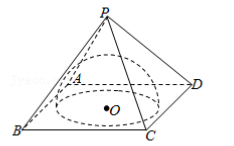
如图, 正四棱锥 P﹣ ABCD 的每个顶点都在球 M的球面上, 侧面 PAB 是等边三角形. 若半球 O 的球心为四棱锥的底面中心, 且半球与四个侧面均相切, 则半球 O 的体积与球 M的体积的比值为
复数 z=(1﹣ 2i)(1﹣ 5i) 的实部为 .



在三棱柱 ABC﹣ A 1 B 1 C 1 中, D 为侧棱 CC 1 的中点, 从该三棱柱的九条棱中随机选取两条, 则这两条棱所在直线至少有一条与直线 BD 异面的概率是()

已知函数 f(x) =tanx﹣ sinxcosx, 则()

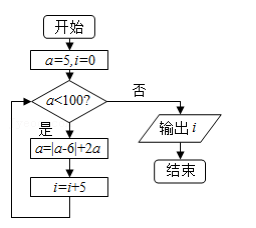
执行如图所示的程序框图, 则输出的 i=()