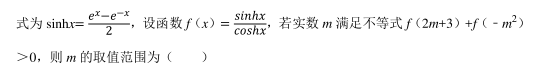已知在△ABC 中， AB＝3， BC＝4，∠ABC=π/3，平面内有动点 E 满足|BE|＝2|AE|． 则数量积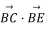
的最大值是
已知在△ABC 中， AB＝3， BC＝4，∠ABC=π/3，平面内有动点 E 满足|BE|＝2|AE|． 则数量积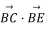的最大值是
已知抛物线 C： x2 ＝2py（p＞0） 的焦点为 F， 点 P（4， 4） 在 C 上， 则|PF|＝
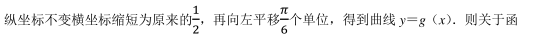
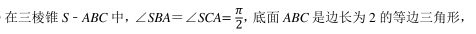
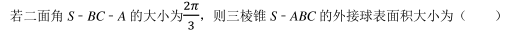
已知 f（x） 是定义在 R 上的偶函数， 且满足 f（1﹣ x） ＝f（1+x）， 当 x∈[0， 1]时， f（x） ＝x 2 ， 则函数 y＝f（x） ﹣ |log4|x||的零点个数为（）
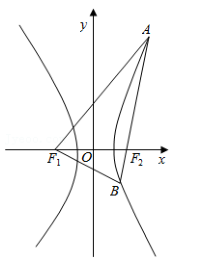
如图， 已知双曲线 C：
（a＞0， b＞0） 的左、 右焦点分别为 F 1 ， F 2 ，过点 F 2 作直线 l 交双曲线 C 的右支于 A， B 两点． 若|AB|＝|AF 1 |， 且Δ F 1 AB～Δ F 2 F 1 B，则双曲线 C 的离心率为（）
已知在△ABC 中， 内角 A， B， C 的对边分别是 a， b， c， 若 2ccosB＝2a﹣ b． 且c = √13， b＝3， 则△ABC 的面积为（）
已知 α， β 是两个不同的平面， m， n 是两条不同的直线， 给出下列命题：
①若 α∥β， m⊥α， 则 m⊥β；
②若 m∥n， m⊥α， 则 n⊥α；
③若 α⊥β， m⊥α， 则 m∥β；
④若 m⊥n， m⊥α， 则 n∥α．
其中真命题的有（）
意大利画家达•芬奇提出： 固定项链的两端， 使其在重力的作用下自然下垂， 那么项链所形成的曲线是什么？ 这就是著名的“悬链线问题”， 其中双曲余弦函数 coshx 就是一种特殊的悬链线函数，其函数表达
